объясняется просто тем фактом, что при том же показателе расширения полосы частот коды Адамара обеспечивают большее разнесение, чем ортогональные блоковые коды. Альтернативно можно сказать, что коды Адамара обеспечивают лучшую эффективность использования полосы частот, чем ортогональные блоковые коды. Необходимо напомнить, однако, что при малых ОСШ код с низким разнесением превосходит коды с большим разнесением, как следствие того факта, что в канале с релеевскими замираниями имеется оптимальное распределение суммарного принимаемого ОСШ по сигналам разнесения. Следовательно, кривые ортогональных блоковых кодов пересекают сверху кривые кодов Адамара в области малых ОСШ (высокая вероятность ошибки).

Метод 4: Каскадирование. В этом методе мы начнем с двух кодов: один двоичный и другой недвоичный. Двоичный код - внутренний блоковый код {п,к) с постоянным весом (нелинейный). Недвоичный код, который может быть линейным, является внешним. Чтобы отличать его от внутреннего кода, мы используем большие буквы, например {N,K) код, где N и К измеряются числом символов -ичного алфавита. Объем q алфавита, через который определяется внешний код, не может быть больше, чем число слов внутреннего кода. Внешний код, если он определяется через кодовые слова двоичного внутреннего кода -ичными символами, это новый код.

Важный частный случай получается, когда qr = 2* и объем внутреннего кода выбирается равным 2*. Тогда число слов = 2** и каскадная структура образует {пМ,кК) код. Показатель расширения полосы частот этого каскадного кода определяется произведением показателей расширения полосы частот внутреннего и внешнего кодов.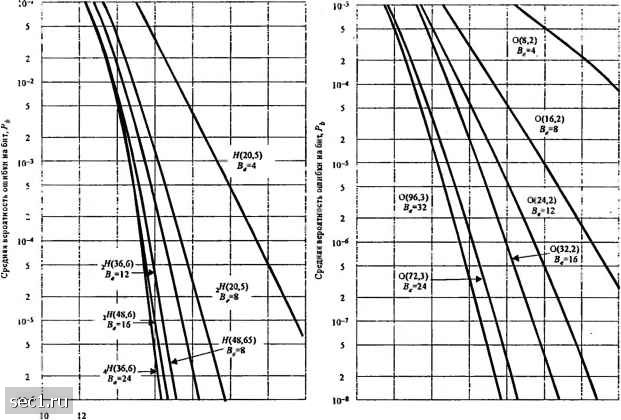

14 16 18

Cpejmet ОСШ (дБ)

Рис. 14.6.6. Характеристики кода Адамара

14 16 18

СредеееОСШ Гд (дБ)

Рис. 14.6.7. Характеристики блоковых ортогональных кодов

10-5

10-«

10-«

10 12 14 16 \s

Ср«янееОСШу4 №)

Рис. 14.6.8. Сравнение характеристик кодов Адамара и бпокйвых ортогональных кодов

Теперь МЫ покажем выгоду в качестве, получаемую в канале с релеевскими замираниями посредством каскадного кода. В частности мы сконструируем каскадный код, в котором внешний код является к -дуальным (недвоичным) свёрточным кодом, а внутренний код является или кодом Адамара, или блоковым ортогональным кодом. То есть мы рассматриваем А:-дуальный код с М-ич-ными (М = 2*) ортогональными сигналами для модуляции, как каскадный код. Во всех случаях при расчетах мы предполагаем декодирование по Витерби мягких решений.

Вероятность ошибки для Л-дуального свёрточного кода получена при дифференцировании передаточной

функции кода, определенной (8.2.39). Для Л-дуального кода без повторений со скоростью 1/2 вероятность ошибки на бит (для случая, когда кодовый выходной к-битовый символ Л-дуального кода отображается в один из М = 2* ортогональных кодовых слов) ограничена сверху

(4.6.21)

m 4

где PjW дано (14.6.12).

Для примера, 2-дуальный код со скоростью 1/2 может использовать 4-позиционный ортогональный код 0(4,2) в качестве внутреннего. Показатель расширения полосы частот для результирующего каскадного кода равен, конечно, произведению показателей расширения полосы частот внутреннего и внешнего кодов.

Так, в этом примере скорость внешнего и внутреннего кодов равна 1/2. Следовательно, = (4/2) (2)= 4.

Заметим, что если каждый символ Л-дуального кода повторить г раз, то это эквивалентно использованию ортогонального кода с разнесением L = г. Если мы выберем г = 2 в выше приведённом примере, результирующий ортогональный код обозначается 0(8,2) и показатель расширения полосы частот для 2-дуального кода со скоростью 1/2 равно B=S. Следовательно, слагаемые PjC") (14.6.21) следует заменить на PimL), если ортогональный код имеет /--кратное разнесение. Поскольку код Адамара имеет «эффективное разнесение» fij,,, то следует, что при использовании кода Адамара в качестве внутреннего кода с А-дуальным кодом в качестве внешнего, еще справедлива верхняя граница для вероятности ошибки на бит результирующего каскадного кода, определенного (14.6.21), если PjO") заменить на /jdmm)- этими изменениями была

рассчитана верхняя граница вероятности ошибки на бит, определяемая (14.6.21), для Л-дуального сверточного кода со скоростью 1/2 с кодом Адамара или блокового ортогонального кода,как внутреннего. Результирующий каскадный код имеет показатель расширения полосы в два раза больший, чем показатель расширения полосы внутреннего кода.

Сначала рассмотрим выигрышные качества, обусловленные каскадным объединением кодов. Рис. 14.6.9 иллюстрирует качество Л-дуального кода с ортогональным блоковым кодом в качестве внутреннего по сравнению с качеством ортогонального блокового кода для показателя расширения полосы частот В=4, 8, 16 и 32. Выигрыш качества, обусловленный каскадированием, очень впечатляет. Например, при вероятности ошибки 10"* и B=S Л-дуальный код превосходит ортогональный блоковый код на 7,5 дБ. Этот

выигрыш можно приписать увеличению разнесения (увеличению минимального расстояния), получаемому посредством каскадирования. Аналогично рис. 14.6.10 иллюстрирует качество двух Л-дуальных кодов с кодом Адамара в качестве внутреннего кода для B=S и 12.

«с

10 5

10-5 5

10-< 5

10-1 5

2 10-«

10 12 14 16 18

Среднее ОСШ Уд (дБ)

Рис. 14.6.9. Сравнение характеристик блоковых ортогональных кодов и каскадных кодов, содержащих Х:-дуальный код