Рассмотрим модель системы связи, показанную на рис. 14.6.1.

Модулятор имеет q- ичный ортогональный ЧМ алфавит. Кодовые слова с длиной блока п отображаются в сигналы путем выбора и частот из алфавита q частот. Демодуляция выполняется пропусканием сигнала через банк из q согласованных фильтров, за которыми следуют квадратичные детекторы. Считается, что выполняется декодирование мягких решений. Выходы квадратичных детекторов демодулятора соответствующим образом комбинируются (суммируются) с равными весами для формирования Л/ величин для решения, соответствующего М возможным переданным кодовым словам.

Чтобы рассчитать объединенную верхнюю границу для вероятности ошибки в канале с релеевскими замираниями и АБГШ, мы сначала рассчитаем вероятность ошибки на бит, включая расчёт величины для решения f/,, соответствующей переданному кодовому слову, и любых из остальных Л/-1 величин для решений, соответствующих остальным кодовым словам. Пусть f/,-другая величина для решения и пусть U и t/, имеют / общих частот. Поскольку вклад ъ U, и U~ этих / частот идентичен, он исчезает при формировании разности U-U для принятия решения. Так как две величины для решения различаются в и-/ частотах, вероятность ошибки равно той, которая получается для двоичной ортогональной системы ЧМ с порядком разнесения п-1. Точное выражение для этой вероятности ошибки даётся (14.6.4), где р = \/{2+у), а - среднее ОСШ на

частоту. Для упрощения мы используем границу Чернова для этого двоичного перехода, ведущего к ошибке, и определяемого (14.6.2), т.е.

R(u,,u2\l)<M\-pt. (14.6.22)

Теперь проведем усреднение по ансамблю двоичных систем связи. Имеется q" возможных кодовых слов, из которых мы случайно выбираем два кодовых слова. Каждое кодовое слово выбирается с равной вероятностью. Вероятность того, что два случайных выбранных кодовых слов имеют вместе / частот, равна:

Р(/) =

"YiY

(14.6.23)

Если усредним (14.6.22) по / с вероятностями (14.6.23), мы получим

а5Ш=1;а(у,.у.И)

(14.6.24)

-11+<я-Ы-р)]

В заключении найдем объединенную границу вероятности ошибки системы связи, которая использует М = 2* случайно выбираемых кодовых слов

< (М - 1)ЩДД) < М РММ. (14.6.25)

Комбинируя (14.6.24) и (14.6.25), мы получаем верхнюю границу для средней вероятности ошибки на символ

iMffo-R.) (14.6.26)

где =к/п - скорость кода, а - предельная скорость, определяемая так:

1 + 4{д-1)р{\-рУ

График Ro как функции у, показан на рис. 14.6.13 для q=2, 4 и 8.

(14.6.27)

(14.6.28)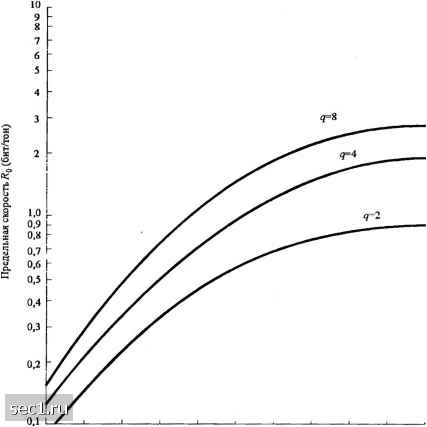

о 2 4 б 8 10 12 14 16

Среднее ОСШ тона (дБ)

Рис. 14.6.13. Предельная скорость как функция от

для канала с релеевскими замираниями

18 20

Более интересная форма (14.6.26) может получиться, если выразить i через ОСШ на бит. В частности (14.6.26) можно выразить так

4<2-*f*(->-i] (14.6.29)

где по определению

Ус Ус

l + 4{q-\)p{\-p)

(14.6.30)

Графики g{q,yj) с параметром q, как функция у построены на рис. 14.6.14.

0,22 -

0.21 -0,20 0.19 0.18

0.17 -

0.16 .

0.15 -

0.14 -

0.13 -0.12

O.Il -

0.10 -

0.09 -

0,08 i.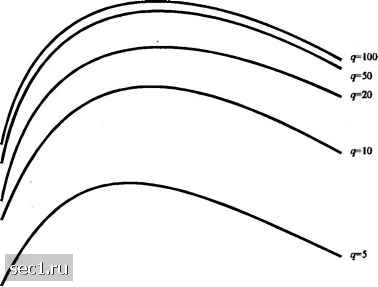

0.07 L

0 1 2 3 4 5

Среднее ОСШ тона (дБ)

Рис. 14.6.14. График функции g(<7,Yj,)

Для начала заметим, что имеется оптимальное значение для каждой величины q, которая минимизирует вероятность ошибки. Для больших q эта величина примерно равна у. = 3 (5 дБ), что согласуется с нашими прежними наблюдениями для обычного

квадратичного сложения. Далее, если ->оо, функция (,7) стремится к пределу, который равен

lim (,yJ = g„(Yj = =log.

q-*<a

4(1 + yJ

Значение gjy), рассчитанное при Yc = 3, равно

g„(3)=maxg„(Yj=0,215.

(14.6.31)