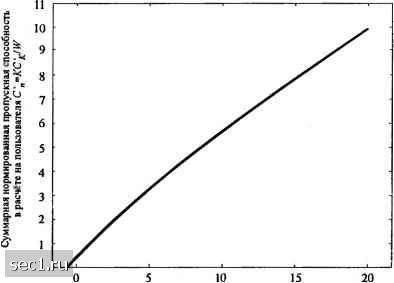Рис. 15.2.2. Суммарная нормированная пропускная способность как функция от для FDMA

В системе TDMA каждый пользователь передает по каналу в полосе W на интервале времени 1/АГ со средней мощностью КР. Следовательно, пропускная способность на пользователя равна

(15.2.7)

ЧТО равно пропускной способности TDMA системы. Однако с практической точки зрения мы должны подчеркнуть, что в TDMA передатчики не всегда могут поддерживать мощность передачи КР, если К очень велико. Следовательно имеется практический предел, выще которого мощность передатчика нельзя увеличить с ростом К.

В CDMA системе каждый пользователь передает псевдослучайный сигнал с полосой W и средней мощностью Р. Пропускная способность системы зависит от уровня сотрудничества между К пользователями. В экстремальном случае имеем CDMA без сотрудничества, когда приёмник для каждого сигнала пользователя не знает рассеянный сигнал других пользователей или выбирается с игнорированием этого знания в процессе демодуляции. Тогда сигналы других пользователей проявляются как интерференция на приёме у каждого пользователя. В этом случае приёмник многих пользователей состоит из банка К приёмников отдельных пользователей. Если предположим, что псевдослучайный сигнал каждого пользователя гауссовский, тогда сигнал каждого пользователя поражается гауссовской интерференцией мощностью {К-\)Р и аддитивным гауссовским шумом мощности WNq . Следовательно, пропускная способность на пользователя

WN.+{K-\)P

или, что эквивалентно

Рис. 15.2.3 иллюстрирует зависимость Q/W от Ц,/ с параметром К.

(15.2.8)

с" е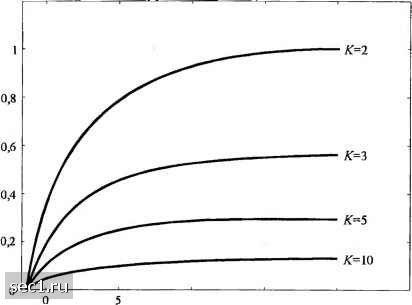

Рис. 15.2.3. Нормированная пропускная способность как функция от ддя несогласованной CDMA

При большом числе пользователей мы можем использовать аппроксимацию 1п(1 + х) < X. Следовательно,

О. с; Ц,/М,

(15.2.10)

или, что эквивалентно.

C„<log,e-

(15.2.11)

fSjN, In 2 SJN, In 2 В этом случае мы видим, что суммарная пропускная способность не увеличивается с ростом К, как при FDMA и TDMA. С другой стороны, предположим, что К пользователей сотрудничают посредством синхронной передачи во времени и приёмник многих пользователей знает рассеяние сигналов всех пользователей и совместно демодулирует и детектирует все сигналы пользователей. Пусть каждый пользователь имеет скорость передачи i, 1</<ЛГ, и кодовый словарь, содержащий набор из 2" кодовых слов мощностью Р. На каждом сигнальном интервале каждый пользователь выбирает произвольное кодовое слово, скажем, X, из своего собственного кодового словаря и все пользователи передают их кодовые слова одновременно. Таким образом, декодер на приёме наблюдает

(15.2.12)

где Z - вектор аддитивного шума. Оптимальный декодер выносет решение по К кодовым словам, одно по каждому кодовому словарю, в пользу слов, которые образуют векторную сумму, которая наиболее близка по Евклиду к принимаемому вектору Y.

Достигаемый К -мерный диапазон скоростей для К пользователей в канале с АБГШ, при условии равенства мощностей каждого пользователя, дается следующим уравнением:

Р

Д.<Ж1оЕ,

(15.2.13)

R,+Rj<Wlog2

l<iJ<K

(15.2.14)

(15.2.15)

Для частного случая, когда все скорости одинаковы, неравенство (15.2.15) доминирует

относительно других К-1 неравенств. Отсюда следует, что если скорости {, 1 </</г}

для К сотрудничающих синхронных пользователей выбираются так, чтобы вместиться в область пропускной способности, определенную выщеприведенными неравенствами, тогда вероятность ошибки для К пользователей стремится к нулю, когда длина кодового блока п стремится к бесконечности.

Из приведенного обсуждения мы заключаем, что сумма скоростей К пользователей становится неограниченной с ростом К. Следовательно, при сотрудничающих синхронных пользователей пропускная способность CDMA имеет форму похожую на форму FDMA и TDMA. Заметим, что если все скорости пользователей CDMA системы выбраны одинаковыми и равными R, тогда (15.2.15) дает

Л<-logj

(15.2.16)

WN,,

что идентично ограничению скорости для FDMA и TDMA. В этом случае CDMA не обеспечивает большую скорость, чем FDMA и TDMA. Однако, если скорости К пользователей выбираются неравными так, чтобы неравенства (15.2.13)-{15.2.15) выполнялись, тогда возможно найти такие точки в достижимой области скоростей, что сумма скоростей К пользователей CDMA превосходит пропускную способность FDMA и TDMA.

Пример 15.2.1. Рассмотрим случай двух пользователей в системе CDMA, которые используют кодированные сигналы, описанные выше. Скорости двух пользователей должны удовлетворять неравенствам

R,<W\og2

R+R<Wlog,

где Р- средняя переданная мощность каждого пользователя, а W- полоса частот сигнала. Определим область пропускной способности, для системы CDMA с двумя пользователями.

Область пропускной способности для CDMA с двумя пользователями с кодированными сигналами имеет форму, иллюстрированную на рис. 15.2.4, где

c:=wiog.

/ = 1,2

- это пропускные способности, соответствующие двум пользователям с Р= Р, = Р.