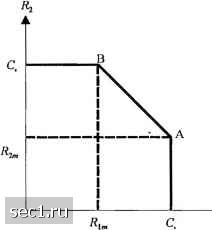Рис. 15.2.4. Область пропускной способности гауссовского канала с CDMA с двумя пользователями

Заметим, что если пользователь 1 передает с пропускной способностью С,, то пользователь 2 может передавать с максимальной скоростью

-q = w\og,

P + WN

(15.2.17)

что иллюстрируется на рис. 15.2.4 точкой А. Этот результат имеет интересную интерпретацию. Мы видим, что i?, соответствует случаю, когда сигнал пользователя 1 рассматривается как эквивалентный аддитивный шум при детектировании сигнала пользователя 2. С другой стороны, пользователь 1 может передавать с пропускной способностью С,, поскольку приёмник знает передаваемый сигнал пользователя 2 и. следовательно, он может ограничить его влияние при детектировании сигнала пользователя 1.

Вследствие симметрии аналогичная ситуация существует если пользователь 2 передает с пропускной способностью Cj . Тогда пользователь 1 может передавать с максимальной скоростью R = R2„, что иллюстрируется на рис. 15.2.4 точкой В. В этом случае мы имеем аналогичную интерпретацию, как выше с заменой ролей пользователей 1 и 2.

Точки А и В соединяются прямой линией. Легко видеть, что эта прямая линия является границей достижимой области скоростей, поскольку любая точка линии соответствует

максимальной скорости Wlog2(l + 2Р/WNq), которую можно достичь простым делением

во времени канала между двумя пользователями.

В следующем разделе мы рассмотрим проблему детектирования сигнала для систем CDMA со многими пользователями и оценим качество и вычислительную сложность нескольких структур приёмника.

15.3. множественный доступ с кодовым разделением

Как мы видели ТДМА и FDMA являются методами множественного доступа, при которых канал разделяется на независимые, используемые одним пользователем подканалы, т.е. неперекрывающиеся интервалы времени или частоты, соответственно. В CDMA каждому пользователю предназначается различная адресная последовательность (или сигнал), которую получатель использует для модуляции с рассеиванием информации по всему сигналу. Адресная последовательность также позволяет приёмнику

демодулировать сообщения, переданные многими пользователями канала, которые передают сигналы одновременно и в общем асинхронно.

В этом разделе мы рассмотрим демодуляцию и детектирование CDMA сигналов от многих пользователей. Мы увидим, что оптимальный детектор максимального правдоподобия имеет вычислительную сложность, которая растёт экспоненциально с числом пользователей. Такая высокая сложность служит мотивацией для разработки субоптимальных детекторов, имеющих более низкую вычислительную сложность. В заключении, мы рассмотрим характеристики качества различных детекторов.

15.3.1. Сигналы CDMA и модели канала

Рассмотрим CDMA канал, который делят К одновременных пользователей. Каждому пользователю предназначается адресный сигнал g{t) длительностью Г, где Т-символьный интервал. Адресный сигнал можно выразить так

gM = lLMp{-nTX Q<t<T, (15.3.1)

где 0<w<Z,-l} псевдошумовая (ПШ) кодовая последовательность, содержащая

L чипов, которые принимают значение {±1}, Д/)-импульс длительности 7, а 1[-интервал чипа. Таким образом, мы имеем L чипов на символ T=LT. Без потери общности мы предположим, что все К адресных сигнала имеют единичную энергию:

\lgl{t) = \. (15.3.2)

Взаимная корреляция между парой адресных сигналов играет важную роль для метрик детектора сигнала и его качества. Мы определим следующие взаимные корреляции:

9>M) = \lgM)gjit-t)dt, i<j, (15.3.3)

Pj,{x) = [gMgj(t + T-T)di, i<j. (15.3.4)

Для простоты предположим, что для передачи информации от каждого пользователя используются двоичные противоположные сигналы. Далее, пусть информационная

последовательность от А-го пользователя обозначается где величина каждого

информационного символа может быть +1. Удобно рассмотреть передачу блока символов одинаковой произвольной длины, скажем N. Тогда блок данных от к -го пользователя

Ь,=[3,(1) ... (15.3.5)

и соответствующий эквивалентный низкочастотный сигнал можно выразить так:

= 4\ j;,Mi)g,{t - if), (15.3.6)

i«l

где энергия сигнала на бит. Суммарный передаваемый сигнал от К пользователей можно записать

t)f,s,{t-x,) = J:4%cJLK{i)gXt-iT-x,), (15.3.7)

-=1 к=\ 1=1

где {tj.}-задержки передачи, удовлетворяющие условию 0<х<Т для \<к<К. Без потери общности предположим, что 0x,<tj<...<Tt<7. Это модель переданного

сигнала от многих пользователей в асинхронном режиме. В специальном случае синхронной передачи, х-О для 1<А-<А!. Величины х, фигурирующие в выражениях взаимной корреляции, даваемых (15.3.3) и (15.3.4) также можно, без потери общности, ограничить областью О < т < Г.

Считается, что передаваемый сигнал искажается АБГШ. Следовательно, принимаемый сигнал можно записать так.

r{t) = s{t)+n{t), (15.3.8)

где s{t) определяется (15.3.7), а п{() - АБГШ со спектральной плотностью мощности N„. 15.3.2. Оптимальный приёмник

Оптимальный приёмник определяется как приёмник, который выбирает наиболее правдоподобную последовательность символов {W, 1<п< N,\<k < по

принимаемому сигналу r{t), наблюдаемому на интервале 0<t<NT + 2T. Сначала мы рассмотрим случай синхронной передачи; позже мы рассмотрим асинхронную передачу.

Синхронная передача. При синхронной передаче каждый пользователь производит точно один символ на сигнальном интервале рассматриваемого пользователя. При белом гауссовском шуме в канале достаточно рассмотреть принимаемый сигнал на одном сигнальном интервале, 0<t<T и определять оптимальный приёмник. Таким образом r{i) можно выразить так

Kt) = T.yliM)gM+f<il 0<t<T. (15.3.9)

Оптимальный максимально правдоподобный приёмник вычисляет функцию правдоподобия

л(ь)=/;

dt (15.3.10)

и выбирает информационную последовательность которая

минимизирует А(Ь). Если мы раскроем интеграл в 15.3.10, то получим

А(Ь) - llr4t)dt -2Jyl%b,il)l%it)g,{f)dt +

(15.3.11)

Видим, что интеграл от r{t) является общим для всех возможных последовательностей {.(l)} и он не влияет в определении того, какая последовательность передана. Следовательно его можно упустить. Слагаемое

r{t)g,{t)dt, \<к<.К (15.3.12)

Гк =

представляет собой взаимную корреляцию принимаемого сигнала с каждым из К адресными последовательностями. Вместо взаимных корреляторов мы можем использовать согласованные фильтры. Наконец интеграл, включающий gt) и gj{t) даёт