Щелевая 1-Настойчивий

Щелевая Ненастойчивый

20 -

10 -

о g-

2 -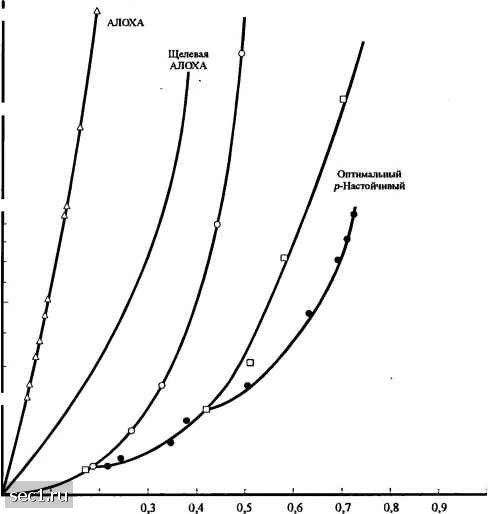

0,4 0,5 Проходимость S

Рис. 15.4.7. Проходимость в обмен на задержку (моделирование при а=0,01) [Kleinrock и Tobagi (1975), © IEEE]

Для сравнения также показана зависимость задержки от характеристик прохождения для протоколов щелевой и бесщелевой Алохи. При этом моделировании только вновь генерированные пакеты считались независимыми и с пуассоновским распределением. Столкновения и неравномерно распределенные случайные ретрансляции обходятся без последующих предположений. Результаты этого моделирования иллюстрируют превосходство качества р-настойчивых и ненастойчивых протоколов относительно протоколов Алохи. Заметим, что значение, обозначенное на графике как "оптимальное /-настойчивое" получено путем нахождения оптимального значения р для каждого значения проходимости. Мы видим, что для малых значений проходимости 1-настойчивой

[р = l) протокол является оптимальным.

15.5. библиографические замечания и ссылки

FDMA была основной схемой для множественного доступа, которая долгое время использовалась в телефонных систем связи для аналоговой передачи голоса (?). С наступлением цифровой передачи речи, использующей ЖМ, ДИКМ и другие методы кодирования речи, TDMA заменила FDMA, как основная схема множественного доступа в связи. CDMA и методы случайного доступа в целом были разработаны за последние три десятилетия, сначала для беспроводной передачи сигналов и в канальных сетях в свободном пространстве.

Теория информации систем со многими пользователями имеет дело с базовыми информационно-теоретическими ограничениями при кодировании источников для многих пользователей и канального кодирования и модуляции для каналов с множественным доступом. Существует большое количество литературы по этим темам. В контексте нашей трактовки методов множественного доступа читатель может найти особо относящийся к делу материал в статьях Ковера (1972). ЭльГамаля и Ковера (1980), Бергманса и Ковера (1974) и Хая (1984). способность сотовых систем CDMA была рассмотрена в статье Гильхоузена и др. (1991).

Демодуляция и детектирование сигналов в системах со многими пользователями привлекают особое внимание в последние годы. Читатель отсылается к статьям Верду (1986 а-с, 1989), Лупаса и Верду (1990), Хая и др. (1990 а,Ь), Пур и Верду (1988), Занга и Браду (1993) Звонара и Браду (1995). Ранние работы по синтезу сигналов и демодуляции для систем связи со многими пользователями можно найти в статьях Ван Эттена (1975, 1976), Хорвуда и Гаглиарди (1975), и Кайе и Джордже (1970).

Система ALOHA, которая была одна из самых ранних систем со случайным доступом трактуется в статьях Абрамсона (1970, 1977) и Робертса (1975). Эти статьи содержат анализ проходимости для щелевых и не щелевых систем. Исследования стабильности касательно протоколов ALOHA можно найти в статьях Карлеиала и Хеллмана (1975), Жеза и др. (1988) и Месси (1988). Устойчивые протоколы, основанные на трёх алгоритмах для каналов со случайным доступом были впервые даны Капетанакисом (1977). Протоколы множественного доступа с обнаружением несущей, которые мы описали, принадлежат Клейнроку и Тобаджи (1975). Наконец, мы упомянем ШЕЕ Press book, под ред. Абрамсона (1993), который содержит набор статей, имеющих дело с системами связи со множественным доступом.

задачи

15.1. При определении сигналов CDMA и моделей типа, описанных в разделе 15.3.1, мы предположили, что принимаемые сигналы вещественны. Для К>1 это предположение предполагает фазовый синхронизм на всех передатчиках, что не очень реально в практических системах. Чтобы представить слу-чай когда 1)азы несущих не синхронизированы мы должны просто изменеть адресные сигналы дая К пользователей, определенные (15.1.1), на комплексные в виде

g,it) = cfa,{n)p{t-nTЛl<k<K,

где 9 представляет постоянный фазовый сдвиг на к-м передатчике, как это видится общим приёмником.

а По данной комплексной форме адресных сигналов, определите форму оптимального МП приёмника, который вычисляет корреляционные метрики, аналогично (15.3.15).

b повторите на.хождение оптимального МП детектора для асинхронной передачи, являющейся аналого.м (15.3.19).

Основополагающая работа [81] по теории линейного разделения сигналов многих пользователей выполнена Д.В. Агеевым в 1935 г. (прп).

15.2. Рассмотрите TDMA систему, когда каждый пользователь ограничен переданной мощностью Р, независимо от числа пользователей. Определите пропускную способность на пользователя С и обпито

пропускную способность КС,. Изобразите С и КС, как функцию от " прокомментируйте

результат при АГ -> оо.

15.3. Рассмотрим систему ГОМА при К = 2 пользователей в канале с АБГШ, где пользователю 1 предназначается полоса I*, =aW, а пользователю 2 предназначается полоса Wi-afV, где 0<а1. Пусть Р и Рз - средние мощности двух пользователей.

а Определите пропускные способности С\ и Cj двух пользователей и их сумму С -С\-С\, как функцию от а. На двумерно.м графике зависимости скорости R2 от изобразите трафик точек ip\,C при изменении « в пределах О < а 1.

b Напомним, что скорости двух пользователей должны удовлетворять условиям

Л, < If, log.

/?2<W2l0g2

1 + -

Определите с>мл1арную пропускную способность С, когда P,/a = P2/(l-a)=P, +Р, и затем покажите, что максимальная скорость достигается, когда а/ (l - а) = Р г = i /*2 •

15.4. Рассмотрите систему TDMA с К = 2 пользователями в кана.пе с АБГШ. Предположите, что два передатчика офаничены по пиковой мощности Р, и и пусть пользователь 1 передает 100а% возможного времени, а по.1ьзователь 2 передает 100(1-а)% времени. Имеющаяся в распоряжении no.i6ca частот равна IV .

л Определите пропускные способности С{ и и С = CJ + С2 как функции от а. b Нарисуйте графики точек (Cj.C,) при изменении а в области О < а < 1.

15.5. Рассмотрите систему TDMA с К = 2 пользователями в канале с АБГШ. Предположите, что два передатчика офаничены по средней мощности Р, и и пусть пользователь 1 передает 100а% возможного

вре&1ени, а пользователь 2 передает 100(l-a)% времени. Имеющаяся в распоряжении патоса частот

равна IV .

•л Определите пропускные способности С{ и С2 н С = С{ +€2 как функции от а.

b Нарисуйте фафики точек (Cj.Cf) при изменении а в области О а < 1.

с В чём схожесть между этим решением и решением для системы FDMA из задачи 1S.3.

15.6. Рассмотрите синхронный канал с множественным доступом при наличии двух пользователей и с1лресных последовательностей, показанных на рис. Р15.6.

-АВ Рнс. Р15.6

Параметр АО описывает относитедьную мощность двух пользователей, а О< Л 1 описывает степень корре-ляции межоу сигналами. Пусть