DE[diX„X)]--Z E[d(x„x,)] = E[dix,x)], (3.4.4)

где последнее равенство следует из предположения, что исходный процесс является стационарным.

Теперь предположим, что мы имеем источник без памяти с непрерывно-амплитудным выходом X, который имеет ФПВ отсчёта р(х), квантованный амплитудный алфавит X и

меру искажения на отсчёт d

Xi,Xi}, где леХи хеХ. Тогда минимальная скорость в

битах на отсчёт, требуемая для представления выхода X источника без памяти с искажением, меньшим или равным D, называется функцией скорость-искажение и определяется как

Я(0)= min /(Х,Х), (3.4.5)

p(.v.v)/:l,/(.\.\)</J

где /(Х,Х) - средняя взаимная информация между X и X. Вообще, скорость R(D) уменьшается при увеличении D или, наоборот, R(D) увеличивается при уменьшении D.

Для гауссовской модели непрерывного по амплитуде информационного источника без памяти Шеннон доказал следующую фундаментальную теорему.

Теорема: Функция скорость-искажение для гауссовского источника без памяти (Шеннон, 1959а). Минимальная скорость кодирования, необходимая для представления выхода дискретного во времени, непрерывного по амплитуде гауссовского источника без памяти, при использовании в качестве меры искажения среднеквадратической ошибки на символ (односимвольная мера искажения)

Iog,(a;-/D) iO<D<a,),

где а/ - дисперсия выхода, гауссовского источника

Заметим, что (3.4.6) подразумевает, что, если искажение D>a, никакой информации передавать не нужно. Конкретно при D = a для реконструкции сигнала доста- \

точно воспроизвести нули. При D > а/ для

реконструкции сигнала мы можем использовать статистически независимые гауссовские шумовые выборки с дисперсией

D-a/. График функции R{D) представлен на рис. 3.4.1,

Функция скорость-искажение RD) источника связана со следующей основной теоремой кодирования источника в теории информации.

(3.4.6)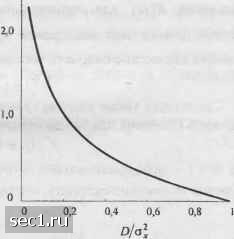

Рис. 3.4.1. Функция скорость-искажение для непрерывного по амплитуде гауссовского источника без памяти

Теорема: Кодирование источника с заданной мерой искажения (Шеннон, 1959а).

Существует схема кодирования, которая отображает выход источника в кодовые слова так, чго для любого данного искажения D минимальная скорость R{D) бит на символ (на

отсчёт) источника является достаточной для восстановления исходного сигнала со средним искажением, которое является произвольно близким к D.

Это очевидно, потому что функция скорость-искажение R{D) для любого источника представляет нижнюю границу скорости источника, которая является возможной для данного уровня искажения.

Вернёмся к результату в (3.4.6) для функции скорость-искажение гауссовского источника без памяти. Если мы поменяем функциональную зависимость между. D и мы можем выразить Dg через R как

D(R) = 2-"a/. (3.4.7)

Эта функция называется функцией искажение-скорость для дискретного во времени гауссовского источника без памяти

Если искажение в (3.4.7) выразить в децибелах, мы получаем

101og,o DiR) = -6 + 101og.o а/. (3.4.8)

Заметим, что среднеквадратическое искажение уменьшается со скоростью 6 дБ/бит.

Явных выражений для функции скорость-искажение для негауссовских источников без памяти не существует. Однако имеются полезные верхние и нижние границы функции скорость-искажение для произвольного дискретного по времени, непрерывного по амплитуде источника без памяти. Верхняя граница даётся следующей теоремой.

Теорема: Верхняя граница для R{D). Функция скорость-искажение непрерывного по амплитуде источника без памяти с нулевым средним и конечной дисперсией ст/ при использовании среднеквадратичной меры искажений ограничена сверху величиной

R(D) <-log, (0<D<cr/). (3.4.9)

Доказательство этой теоремы дано Бергером (1971). Подразумевается, что гауссовский источник требует максимальную скорость кодирования среди всех других источников при заданном уровне среднеквадратической ошибки. Следовательно, функция скорость-искажение R(D) для произвольного непрерывного источника без памяти с нулевым

средним и конечной дисперсией а удовлетворяет условию R{D)< R(D). Аналогично

функция искажение-скорость того же источника удовлетворяет условию

D(R)<D(R) = 2--"a\ (3.4.10)

Существует также нижняя граница функции скорость-искажение. Её называют нижней границей Шеннона для среднеквадратической ошибки искажения, и она определяется так:

R\D) = hiX)-log,2neD, (3.4.11)

где h(X) - дифференциальная энтропия источника без памяти с непрерывной амплитудой. Функция искажение-скорость, соответствующая (3.4.11), равна

D-(/?) = -2-"-"<-Ч. (3.4.12)

2тге

Следовательно, функция скорость-искажение для произвольного источника без памяти с непрерывной амплитудой ограничена сверху и снизу: щ

R\D)<RiD)RiD), (3.4.13)

и соответствующая функция искажение-скорость ограничена:

D\R)<D(R)<D(R). (3.4.14)

Дифференциальная энтропия гауссовского источника без памяти

/z,W = ilog3 27rea/, (3.4.15)

так что нижняя граница R(D) в (3.4.11) уменьшается до RiD). Теперь, если выразить

D (R) в децибелах и нормировать к а =1 [или деля D\R) на а/], мы получаем из (3.4.12)

10 log.o D*(R) = -6R- 6[h (Х) - h(X)] (3.4.16)

или, что эквивалентно,

10 log, о 1 = б[\ {X) - КХ)] дБ = 6[R(D)-R* т дБ. (3.4.17)

Соотношения в (3.4.16) и (3.4.17) позволяют сравнивать нижнюю границу искажений с верхней границей, которая определяет искажения для гауссовского источника. Обратим внимание, что D*(R) также уменьшается со скоростью -6 дБ/бит. Мы должны также

отметить, что дифференциальная энтропия h(X) ограничена сверху величиной h{X), как

показано Шенноном (1948b).

В табл. 3.4.1 даны четыре типа ФПВ, которые являются моделями распределения, обычно используемыми для источника сигнала. В таблице даны значения дифференциальной энтропии, различия в скорости (бит на отсчёт) и различия в искажении между верхней и нижней границами. Заметим, что гамма-распределение показывает самое большое отклонение от гауссовского. Распределение Лапласа наиболее близко к гауссовскому, а равномерное распределение занимает второе место по близости среди ФПВ, показанных в таблице. Эти результаты дают некоторое представление о различии между верхними и нижними границами искажений и скорости.

Перед завершением этого раздела рассмотрим гауссовский источник с ограниченной полосой частот со спектральной плотностью

\й (if\>W).

Если выход этого источника дискретизирован с частотой Найквиста. его отсчёты некоррелированны и. так как источник гауссовский, они также статистически независимы.

Таблица 3.4.1. Дифференциальная энтропия и сравнение скорости и искажений четырёх распространённых ФПВ для моделей сигнала

Следовательно, эквивалентный дискретный во времени гауссовский источник является источником без памяти. Функция скорость-искажение для каждого отсчёта дается (3.4.6). Поэтому функция скорость-искажение для белого гауссовского источника с ограниченной полосой частот в бит/отсчёт равна