Пример 3.4.1. Пусть Х\ и Хг являются двумя случайными величинами с равномерной СФПВ:

р(х,,Х2) = р(Х) = -

(ХеС),

(3.4.45)

О (для других X),

где С - прямоугольная область, показанная на рис. 3.4.4. Заметим, что прямоугольник

повёрнут на 45 относительно горизонтальной оси. На рис. 3.4.4 показаны также собственные плотности вероятностир(х\) и р{х2).

а+Ь а-Ь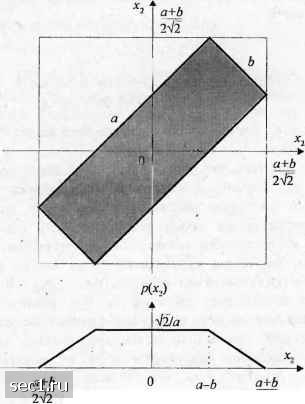

2л/2 2V2

Рис. 3.4.4 Равномерная ФПВ в двух измерениях (Макхоул и др., 1985)

Если мы квантуем xi и хг раздельно, используя одинаковые интервалы квантования длины Д , то требуемое число уровней квантования

(3.4.46)

Следовательно, для кодирования вектора X=[xi хг] потребуется число бит

=R, + R, = log, Ц + log, L,,

(a + bf (3.4.47)

Таким образом, скалярное квантование каждой компоненты эквивалентно векторному

квантованию с общим числом уровней

(3.4.48)

Видим, что это приблихсение эквивалентно покрытию большой площади, которая

охватывает прямоугольник посредством квадратных ячеек, причём каждая ячейка представляет одну из lx областей квантования. Поскольку р(Х)0, за исключением X еС, такое кодирование является расточительным и приводит к увеличению битовой скорости.

Если же мы покроем только область, где р(Х) 9 0. квадратиками, имеющими площадь д-, то общее чцсло уровней, которые образуются, определяется площадью прямоугольника, делённой на Д-, т.е.

L:-. (3.4.49)

Следовательно, разница в битовой скорости при скалярном и векторном методах, квантования равна

K-rog,. (3.4.50)

Для случая, когда а=аь, разница в битовой скорости

-R„ 1,64 бит/вектор. ,

Следовательно, векторное квантование на 0,82 бит/отсчёт лучше, чем скалярное, при тех же искажениях.

Интересно заметить, что линейное преобразование (поворот на 45 ) декоррелирует Х\ и х2 и делает две случайные величины статистически независимыми. Тогда скалярное квантование и векторное квантование достигают одинаковой эффективности. Хотя линейное преобразование может декоррелировать вектор случайных величин, оно не приводит к статистически независимым случайным величинам в общем случае. Следовательно, векторное квантование будет всегда равняться или превосходить по характеристикам скалярный квантователь (см. задачу 3.40).

Векторное квантование применяется при различных методах кодирования речи, включая сигнальные методы и методы базовых моделей, которые рассматриваются в разд. 3.5. В методах, основанных на базовых моделях, таких как линейное кодирование с предсказанием, векторное квантование делает возможным кодирование речи на скоростях ниже 1000 бит/с (см. Бузо и др., 1980; Роукос и др., 1982; Пауль, 1983). Если использовать методы кодирования сигналов, возможно получить хорошее качество речи на скоростях передачи 16 ООО бит/с, что эквивалентно скорости кодирования R-2 бит/отсчёт. За счёт дополнительных вычислительных усложнений в будущем станет возможным использовать сигнальные кодеры, обеспечивающие хорошее качество речи при скорости кодирования R=\ бит/отсчёт.

3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ

За последние 40 лет было разработано много технических приёмов для кодирования аналоговых источников. Большинство из них использованы для кодирования речи и изображений. В этом разделе мы сжато опишем несколько из этих методов и используем кодирование речи как пример при оценивании их характеристик.

Удобно разделить методы кодирования аналоговых источников на три вида. Один вид назван временное сигнальное кодирование. При -этом виде кодирования кодер источника проектируется так, чтобы представить в цифрах временные характеристики сигнала источника. Второй тип кодирования источника - спектральное сигнальное кодирование. В этом случае сигнал обычно подразделяется на различные частотные полоски и либо сигнал каждой полоски, либо его спектральные характеристики кодируются для передачи. Третий тип кодирования источника базируется на математической модели источника, и он называется кодирование на базовой модели.

3.5.1. Временное сигнальное кодирование

Имеется несколько технологических приёмов кодирования источника, которые используют временные характеристики сигнапа. Наиболее широко использующийся метод описьшается в этом разделе.

Импульсно-кодовая модуляция (ИКМ). Пусть x(/) обозначает реализацию сигнала, выдаваемого источником, и пусть x„ обозначает отсчёт, взятый со скоростью стробирования fs>2W, где W- на!ивысщая частота в спектре x(t).

В ИКМ каждый отсчёт сигнала квантуется в один из 2 уровней, где i?-число двоичных цифр, используемых для представления кан<дого отсчёта. Следовательно, скорость источника равна Rбит/с.

Процесс квантования мол<но представить математически как

х„=х„+„, (3.5.1)

где S;, представляет квантованное значение х„. а q„ - ошибку квантования, которую мы трактуем как аддитивный шум. Предположим, что используется равномерное квантование, имеющее характеристику вход-выход, показанную на рис. 3.5.1, тогда шум квантования хорошо характеризуется статистически равномерной ФПВ

р(д) = Т -A<q<A, (3.5.2)

где размер шага квантования А = 2

Выход ▲

7Д/2-5ДД-ЗА/2-

Вход

-ЗД -2Д -Д.оцО 010

--ЗД/2 --5Ш -7Д/2

2Д ЗД

Рис. 3.5.1. Характеристика вход-выход для равномерного квантователя

Средний квадрат ошибки квантования

Eiq) = -A=x2--". (3.5.3)

Средний квадрат ошибки в децибелах равен

lOlgA =101g(;2x2 ")--6J?-10,8 дБ. (3.5.4)

Заметим, что шум квантования уменьшается на 6 дБ на каждый используемый в

ИКМ, ДИКМ (дифференциальная ИКМ) и АДИКМ (адаптивная ДИКМ) относятся к технике кодирования источника. Они не являются методами цифровой модуляции.