квантователе бит. Например, 7-битовый квантователь вызывает мощность шума квантования в -52,8 дБ.

Для многих сигналов источника, таких как речевые сигналы, характерно то, что маленькие уровни сигнала появляются более часто, чем большие. Однако, равномерный квантователь обеспечивает одинаковые расстояния меходу последовательными уровнями во всём динамическом диапазоне сигнала. Лучший подход - это использовать неравномерный квантователь. Характеристики неравномерного квантователя обычно получают пропусканием сигнала через нелинейное устройство, которое сжимает уровни сигнала, поступающие затем на равномерный квантователь.

Например, логарифмический сжиматель (компрессор) имеет амплитудную характеристику вход-выход в виде

1ов(1-Ьдх)

(3.5.5)

log(l-t-i)

где x < 1 - амплитуда входа, у - амплитуда выхода, р. - параметр, который выбирается так, чтобы получить требуемую характеристику компрессии. Рисунок 3.5.2 иллюстрирует характеристики компрессии для некоторых значений ц случаю отсутствия компрессии.

Величина ц О соответствует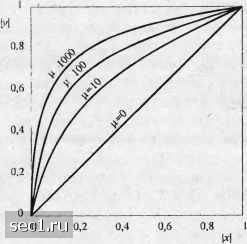

Рис.3 5.2. Амплитудная характеристика вход-выход для логарифмического компрессора

Величина р. 255 принята в качестве стандарта в США и Канаде при кодировании сигналов речи. Эта величина ведёт к уменьшению мощности шума квантования относительно равномерного квантования приблизительно на 24 дБ, как показано Джайантом (1974). Следовательно, 7-битовый квантователь, используемый совместно х логарифмическим компрессором с параметром ц = 255, даёт мощность шума квантования примерно -77 дБ по сравнению с -53 дБ при равномерном квантовании.

При восстановлении сигнала по квантованным значениям используется преобразование (экспандирование), обратное логарифмическому, для декомпрессии амплитуды сигнала. Комбинированную пару компрессор-экспандер называют компандером.

Дифференциальная импульсно-кодовая модуляция (ДИКМ). В ИКМ каждый отсчёт кодируется независимо от других. Однако у многих источников сигнала при стробировании со скоростью Найквиста или быстрее проявляется значительная корреляция между последовательными отсчётами. Другими словами, изменения амплитуды между последовательными отсчётами в среднем относительно малы. Следовательно, схема кодирования, которая учитывает избыточность отсчётов, будет требовать более низкой битовой скорости кодирования для выхода источника.

Относительно простые решения получаются при кодировании разности между последовательными отсчётами, а не самих отсчётов. Поскольку можно ожидать, что разность между отсчётами сигнала меньше, чем действительные значения отсчётов, то потребуется меньшее число бит для представления разностного сигнала. Суть этого общего

подхода - в предсказании текущего значения отсчёта на основе предыдущих р отсчётов. Для конкретности предположим, что х„ означает текущий отсчёт источника, и пусть х„ обозначает предсказанное значение (оценку) для х„, определяемое как

»=Е,»-/- (3-5.6)

Таким образом, х„ является взвешенной линейной комбинацией р отсчётов, а { а, } являются коэффициентами предсказания. Величины {а} выбираются так, чтобы минимизировать некоторую функцию ошибки между х, и х„.

Математически и практически подходящей функцией ошибок является среднеквадратическая ошибка (СКО). В этом случае мы выберем {а,} так, чтобы минимизировать

Р Р

= £(х,)-2а,£(х„х„ ,) + 2;Х«-«.(.-"-.)-

1=1 (-1 7=1

в предположении, что выход источника стационарен (в широком смысле), мы можем выразить (3.5.7) а виде

хФ(о)-2Е«жо+ЁЕ«.« Ф( (3-5-8)

1-1 1=1 J 1

где ф(ш) - автокорреляционная функция последовательности отсчётов сигнала х„. Минимизация <Г, по коэффициентам предсказания {с/,} приводит к системе линейных } равнений

,Ф(-» = Ф(У), 7 = 1,2,...,/.. . (3.5.9)

Таким образом, коэффициенты предсказания определены. Если автокорреляционная функция ()(/) априори не известна, она может быть определена по реализации отсчётов

X,} посредством соотношения

Ф0)-](Е,, У = 1.2,...,р, (3.5.10)

и оценки ф(у) используются в (3.5.9) для нахождения коэффициентов {я,}. Заметим, что

нормирующий множитель MNb (3.5.10) сокращается, когда {п) подставляются в (3 5.9).

Линейные уравнения (3.5.9) для коэффициентов предсказателя называют нормальными уравнениями или уравнениями Юли-Волкера. Имеется алгоритм, разработанный Левинсоном (1974) и Дурбиным (1959) для эффективного решения этих уравнений. Он описывается в приложении А. Мы будем иметь дело с этими уравнениями более детально при последующем обсуждении линейного кодирования с предсказанием.

Имея метод определения коэффициентов предсказания, теперь рассмотрим блок-схему практической системы ДИКМ, показанную на рис. 3.5.3, о. В этой схеме предсказатель встроен в цепь обратной связи, охватывающей квантователь. Вход предсказателя обозначен х„. Он представляет сигнальный отсчёт х„, видоизменённый процессом

Оценка автокорреляционной функции по конечному числу наблюдений заслуживает отдельного исследования, выходящего за пределы нашего обсуждения. Оценка (3.5.10) часто используется на практике.

квантования, а выход предсказателя равен

(3.5.П)

Разность

е,.-х„-%, (3.5.12)

является входом квантователя, а ё„ обозначает его выход. Величина квантованной ошибки предсказания е„ кодируется последовательностью двоичных символов и передаётся через канал в пункт приёма. Квантованная ошибка е, также суммируется с предсказанной величиной x,,, чтобы получить х„ .

в месте приёма создаётся такой же предсказатель, как на передаче, а его выход х, суммируется с е„, чтобы получить х„. Сигнал х„ является входным воздействием для предсказателя и в то же время образует выходную последовательность, по которой с помощью фильтра НЧ, как показано на рис. 3.5.3, Ь, восстанавливается сигнал x{t). Использование обратной связи вокруг квантователя обеспечивает то, что ошибка в х,, - это просто ошибка квантования q„ - е, - е„ и что здесь нет накопления предыдущих ошибок квантования при декодировании. Имеем

- , - е„ 2;, -(х„ -х„) = х„ - х„. (3.5.13)

Стробирующее устройство

Квантоеттель

Предскам 1ель

К переЛ1Т1чку

e,re,ri,r(?,rx,ye+y,rx,rx,-x,rq„ q- ошибка квантования

Предсказатель

К фильтру НЧ

Рис. 3.5.3. {а) Блок-схема кодера ДИКМ; {Ь) Декодер ДИКМ в приёмнике

Следовательно, х„ -х„+ q„. Это означает, что квантованный отсчёт х,, отличается от входа х„ ошибкой квантования q,, независимо от использования предсказателя. Значит, ошибки квантования не накапливаются.

в системе ДИКМ, иллюстрированной рис. 3.5.3, оценка или предсказанная величина х„ отсчёта сигнала х, получается посредством линейной комбинации предыдущих значений х! , к = 1, 2,...,р. как показано в (3.5.11). Улучшение качества оценки можно получить включением в оценку линейно отфильтрованных последних значений квантованной ошибки.