3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ

Кодирование источника является областью интенсивной исследовательской деятельности, начиная с публикаций классических статей Шеннона в 1948 г. и статьи Хаффмена (1952). С годами были получены важные достижения в разработке высокоэффективных алгоритмов сжатия данных источника. В частности, значительными являются научные исследования универсальных кодеров источника и универсальных квантователей, опубликованные Зивом (1985), Зивом и Лемпелом (1977, 1978), Дависсоном (1973), Греем (1975), Дависоном и др. (1981).

Разработки по теории функций скорость-искажение имеются в книгах Галлагера (1968), Бергера (1971), Витерби и Омура (1979), Блейхута (1987) и Грея (1990).

Много работ было выполнено за несколько последних десятилетий по методам кодирования речи. Мы дали здесь обзор этих важных тем. Более исчерпывающая разработка дана в книгах Рабинера и Шафера (1978), Джайанта и Ноля (1984), Деллера и др.(1993). В дополнение к этим публикациям имеются специальные исследования в журнале ШЕЕ Transactions on Communications (апрель 1979 и апрель 1982) и более новые в IEEE Journal on Selected Ereas in Communication (февраль 1988), посвященные кодированию речи. Мы хотим также упомянуть публикацию в IEEE Press книги, содержащей репринты опубликованных статей по кодированию и квантованию сигналов, отредактированные Джайантом (1976).

В последнем десятилетии мы также увидели ряд важных достижений в области векторного квантования. Наша разработка этой темы основывалась на доходчивой работе Макхоула и др.(1985). Всесторонняя разработка по векторному квантованию и сжатию сигналов имеется в книге Гершо и Грея (1992).

ЗАДАЧИ

3.1. Рассмотрим совместный эксперимент из задачи 2.1 с заданной совместной вероятностью р[А,В]. Допустим, мы наблюдаем выходы А,, i = 1, 2, 3, 4 , эксперименте.

a. Определите взаимную информацию для 71,2,3 и/ = 1, 2, 3, 4 в битах.

b. Определите среднюю взаимную информацию /(S; Л). . . ,> •

3.2. Предположим, что выходы Bj, J= 1,2,3, в задаче 3.1 представляют три возможных выходных

слова ДИБП. Определите энтропию источника.

3.3. Докажите, что ln/i<«-l и продемонстрируйте законность этого неравенства, построив кривые Inn

и /7-1.

3.4. x н у являются двумя дискретными случайными величинами с вероятностями р{х = х,у = у) = р(х,у). Покажите, что 1х,у)>0, причем равенство имеет место тогда, и только тогда, когда Ли У статистически независимы.

[Подсказка: используйте неравенство Inw < и -1 для О < w < 1, чтобы доказать, что - 1(х,у) О.]

3.5. Выход ДИБП состоит из возможных символов л:,,д:2,...,лс„ .которые появляются с вероятностями р,,Р2. Р,, соответственно Докажите, что энтропия Н[х) источника не превышает log п. , ,

3.6. Определите дифференциальную энтропию h[x) равномерно распределённой случайной величины x

а~ (0<л;<я), , ., ,.....,. .

О (вне этого интервала)

для следующих трёх случаев:

а) а-1; Ь)а-4; с)а=1/4.

с ФПВ р(х) =

Обратите внимание, что из расчётов следует, что lXj является не абсолютной, а только относительной мерой неопределённости.

3.7. ДИБП имеет алфавит из восьми символов л:,, /= 1, 2,...,8, с вероятностями 0,25; 0,2; 0,15; 0,!2; 0,10; 0,08; 0,05 и 0,05.

a) Используйте процедуру кодирования Хаффмена, чтобы определить двоичный код дпя выхода источника.

b) Определите среднее число R двоичных символов на символ источника.

c) Определите энтропию источника и сравните с R .

3.8. ДИБП источника имеет алфавит из пяти символов у,, / = 1, 2,...,5, каждый из которых появляется с вероятностью 1/5 . Вычислите эффективность равномерного двоичного кода, если:

a) КаждьнЧ символ кодируется отдельно в двоичную последовательность.

b) Два символа вместе кодируются в двоичную последовательность.

c) Три символа вместе кодируются в двоичную последовательность.

3.9. Напомним (3.2.6)

{x,\yj)=l{x,) l[x,\yj).

Докажите, что

a) l{x-yj) = l{yj)-l(yj\x,);

b) l(x,;yj)-/(x,) + j{yj)-/(x„yj),rno l{xr,y,) = -logP{x,.y,).

3.10. Пусть X - геометрически распределённая случайная величина, т.е. р{Х = к) - p{l- р)~\ А = 1,2,3...

a) Найдите энтропию X.

b) Известно, что Х>К, где К - заданное целое положительное число. Чему равна энтропия Х7

3.11. Пусть Jtи / обозначают две совместно распределённые дискретные случайные величины.

a) Покажите, что

H{X)=-Yp{x,yYogP{x),

H{y) = -Y,P[y)iogP{y).

b) Используйте полученный выше результат, чтобы показать, что H[X,Y) < Н[Х] + И{У). Когда наступает равенство?

c) Покажите, что и что равенство имеет место тогда, и только тогда, когда X и У независимы.

3.12. Две двоичные случайные величины X и У распределены согласно совместным вероятностям Р{Х=У=0) Р{Х = О, К - 1) = Р{Х = К = 1) = 1/3. Вычислите Н{Х), Я(У), н[х\У), я[у\х) и Н{Х, У).

3.13. Дан марковский процесс с одношаговой памятью, т.е. такой процесс, что p{x,jX„ ,x„ 2,Jc„ 3,...j = p(jf„.if„ i) для всех п. Покажите, что дяя стационарного марковского процесса

энтропийная скорость определяется через HX„\X„ jj.

3.14. Пусть У = g[X), где g обозначает детерминированную функцию. Покажите, что в общем Н[У) < И[Х). Когда наступает равенство?

3.15. Покажите, что 1{Х; У) = 1{х) + 1{У) - 1{ХУ).

3.16. Покажите, что для статистически независимых событий

H(Xx,X„...,X„) = Y.y

3.17. Покажите, что в канале без шумов (Л]/) = О.

3.18. Покажите, что 1[х;Х2\Х) = H[xJiXi)-Н[Х\ХХ2) и что

н{х,\Хх)>н{х,\х,Х2).

3.19. Пусть является случайной величиной с ФПВ р{х) и пусть у = аХ+Ь - линейное преобразование Л, где анЬ- две константы. Определите дифференциальную энтропию /?(/) через .

3.20. Выходы x,x\x от ДИБП с вероятностями = 0,45, р-О,?) и Рз=0,2 преобразуются линейным преобразованием У = аХ + Ь,гл.& а и b - константы. Определите энтропию H{Y) и поясните влияние преобразования на энтропию сигнала.

3.21. Оптимальный четырёхуровневый неравномерный квантователь для сигнала с гауссовским распределением амплитуд выдаёт четыре уровня я,, 2 > <з ч <4 вероятностями Р\= Pi- 0,3365 и Рз = р4 =0,1635.

a) Определите код Хаффмена, который кодирует отдельные уровни, и определите среднюю битовую скорость.

b) Определите код Хаффмена, который кодирует два выходных уровня вместе, и определите среднюю битовую скорость.

c) Какую минимальную битовую скорость можно получить, кодируя J выходных уровней, когда со .

3.22. Марковский источник первого порядка характеризуется вероятностями состояния р(х,), / = 1, 2, Z, и переходными вероятностями к = \,2, ...,L и k*i. Энтропия марковского

источника Н{х) = У, , где (jtlA:) - энтропия источника при условии, что он находится в

состоянии .

Определите энтропию двоичного источника первого порядка, показанного на рис. 3.22, который имеет переходные вероятности Р{х2\х) = 0,2 и f(jc,x2) - 0,3 [заметим, что условные энтропии Н[Х\Х) и Н[Х\Хт)

определяются двоичными энтропийными функциями Н р(х2Ху) и Н pfxXj) соответственно]. Как

соотносится энтропия марковского источника с энтропией двоичного ДИБП с теми же вероятностями выходных символов и Р{Х2) ?

1-Р(д>,)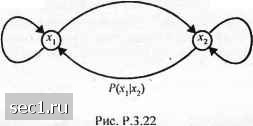

3.23. Источник без памяти имеет алфавит /4 = - 5, - 3, - I, О, 1, 3, 5 с соответствующими вероятностями 0,05; 0,1; 0,1; 0.15; 0,05; 0,25; 0,3 .

a) Найдите энтропию источника.

b) Предположив, что источник квантуется согласно правилу квантования

(-5)=<7(-3)=4,

<7(-1) = ф)-(1) = 0, 9(3) = ?(5)=4,

найдите энтропию квантованного источника.

3.24. Постройте троичный код Хаффмена, использующий выходные символы О, 1 и 2 при кодировании источника с вероятностями выходных символов алфавита {0,05; 0,1; 0,15; 0,17; 0,18; 0Д2; 0,13} . Какова

результирующая средняя длина кодового слова? Сравните среднюю длину кодового слова с энтропией источника. (С каким основанием будете вычислять логарифмы в выражении для энтропии для полностью осмысленного сравнения?).