3.25, Найдите код Лемпела-Зива при кодировании двоичной последовательности источника ООО 100100000011000010000000100000010100001000000110100000001100.

Восстановите исходную последовательность по коду Лемпела-Зива. [Подсказка: Вам потребуются два прохода двоичной последовательности, чтобы принять решение о размере словаря.]

3.26. Найдите дифференциальную энтропию непрерывной случайной величины Хв следующих случаях:

a) Х-случайная величина с экспоненциальным распределением с параметром X > О, т.е.

[Яе (;с>0), О (для других х).

b) -случайная величина с распределением Лапласа с параметром Л. > О, т.е.

R{D) =

с) А-случайная величина с треугольным законом распределения с параметром Х>0, т.е.

(х + \)/х {-Х<х<0), {-Х + Х)/Х {Q<x<X),

О (для других х). I

3.27. Можно показать, что для источника с рапределением Лапласа Уд-(-т) = (2/\.)~е~ функция скорость-искажение с абсолютной величиной меры ошибки искажений d{x,x) - \х-х определяется как

log(X/D) {Q<D<X),

[О {d>x у

(См. Бергер, 1971)

a) Сколько требуется бит/отсчёт для представления выходов источника со средним искажением, не превышающим АУ2?

b) Постройте график R(D) для трёх различных значений X и обсудите влияние изменения X на этих кривых.

3.28. Можно показать, что если Х- непрерывная случайная величина с нулевым средним и дисперсией-о, то её функция скорость-искажение при среднеквадратичной мере искажений удовлетворяет нижней и верхней границам, определяемым неравенствами -

Р(Х)--loglnsD < r{d) < log ja ,

где h(x) означает дифференциальную энтропию случайной величиныХ(см. Ковер и Томас, 1991)

a) Покажите, что для гауссовской случайной величины верхней и нижней границ совпадают.

b) Постройте график для нижней и верхней границ для источника с лапласовским распределением при а-=1.

c) Постройте график для нижней и верхней границ для источника с треугольным распределением при

3.29. Стационарный случайный процесс имеет автокорреляционную функцию Rx() = 4 4е~"со52л/оТ

и известно, что случайный процесс никогда не превышает по амплитуде величину 6. Сколько требуется уровней квантования амплитуды, чтобы гарантировать отношение сигнал/шум квантования не хуже 60 дБ?

3.30. Канал с аддитивным белым гауссовским шумом имеет выход Y-X .V, где X - вход канала, а N шум с ФПВ:

Для случая, когда Jf"- гауссовский белый шум с параметрами Е[Х) = О и (-), определите:

a) условную дифференциальную энтропию h(x\n);

b) среднюю взаимную информацию 1(Х;У).

3.31. ДИБП имеет алфавит из восьми символов х„ / = 1,2,.,.,8 с вероятностями из задачи 5.7. Используйте процедуру кодирования Хаффмена для нахождения троичного кода (с символами 0,1 и 2) для кодирования выхода источника. [Подсказка: прибавьте символ хд с вероятностью Р9=0 и группируйте по три символа на каждом шаге.]

3.32. Определите, существует ли двоичный код с кодовыми словами длиной («,, и,, п, п) = (, 2, 2, 3), удовлетворяющий условию префиксности.

3.33. PaccMOipine диопчнып блоковый код с 2" кодовыми словами одинаковой длимы I (окаАнгс. что неравенство Крафта выполняется для такого кода.

3.34. Покажите, что энтропия л-мерного гауссовского вектора Х-[.\- .vi ....v„] с нулевым средним и матрицей ковариации 1М равна

/y(X)--iog,(2He)"M.

3.35. Рассмотрите ДИБП с равновероятными двоичными вы.чоднымп снмволахм! (0,1). Усганошис мср> пскажстм! как D=P, где /\. - вероятность ошибки при передаче двоичных символов иольювак.ио ч-рез ДВОИЧНЫ!! симметричный канал (ДСК). Тогда функция скороегь-искажсиие равна (Бергер, 1971)

/?(D) = 1 + D log, D + {\D) log. (1 - D), 0 < D = /; < 4.

Постройте фафнк R{D) для 0<D<l/2. *

3.36. Вычислите функцию скорость-искажение для Л/-нчного симметричного канала

/?(D) = log, ЛУ + D log-, D + (1 - D) log-,

Л/ -1

.и1я Л/ 2, 4, 8 и 16. D-P,/- вероятность ошибки.

3.37. Расслютрите пользу от взвешенной СКО как меры пскажсти"!, определенной как

c (X,X) = (X-X) W(X- X) , где W - симметричная, положительно-определённая взвешивающая матрица. Пу-гём факторизации W как \V=IP покажите, что й„(Х,Х) эквивалентно невзвешенпой СКО как меры нскажешиТ i:/,(X,X).

со.чсржащеП преобразованные векторы Х и Х.

3.38. Расс\ютрите стационарную случайную сигнальную последовательность [.\(/01 с нулевым срсдшгм II автокорреляционной функцией

11 (/ = 0),

Ф(0 =

(" = ±1), [О (для других п).

a) Определите коэфф1Щненты предсказания для предсказателя первого порядка с лншмлтзацнсн СКО .ш {.\(/0}, заданной посредством соотношения

.v(/7)=a,.v(;;-l),

I! соответствующее значение минимальной СКО i*, .

b) Повторите (л) для предсказателя второго порядка

.v(/7) = ax[n - l) + chx[n - 2). i

3.39. Рассмотрите кодирование случайных величин А и Х2, которые характеризуются СФПВ рС.1-Д-2), заданной как

, , 15/7

как 1Юказ<1но на рис. Р.3.39. Вычислите б1гговую скорость, требуемую при рав1юмерном раздельном квантовании .Vi и .vi (скалярное квантование) и комбинированном (векторном) квантовании (.v,, .v,). Определ1гге разницу в битовой скорости при я=4А

n.v)

!5 7/.

2" 5"

1<- i"

► V

Рис. Р.3.39

9 56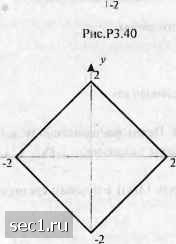

3.40. Рассмотрите кодирование двух случаПных величин и /, которые имеют равномерное распределение в области между двумя квадратами, как показано на рис. Р3.40.

a) Найдите/\{л-) м/АуУ

b) Предположите, что каждая из случайных величии Л и Y квантуется с использованием четырёхуровневого равномерного квантователя. Каково результирующее искажение? Каково результирующее число бит на пару (X, У)?

c) Предположите, что вместо скалярного квантования Аи Умы используем векторный квантователь для достижения того же уровня искажений, как в (Ь). Каково результирующее число битов на вы.ходную пару источника {X, К)?

3.41. Две случайные величины X ч Y распределены равномерно в квадрате, показанном на рис. P3.4I.

a) Найдитеи у; (у).

b) Предположите, что каждая из случайных величин X и ) квантуется посредством четырёхуровневого равномерного квантователя. Каково результирующее искажение? Каково результирующее число бит на пару источника {X, Г)?

c) Предположите, что вместо скалярного квантования X и У мы используем векторный квантователь с тем же числом бит на пару источника (Л, У), что в (й). Каково результирующее искажение для этого векторного квантователя?

Рис. Р3.41