Inkt

s{t)cos--dt.

1 о (4.2.31)

Ансамбль ортонормированных тригонометрических функций

{Jfcos2nkt/T, .j2/f sinlnk t/T

является полным, и, следовательно, ряд (4.2.30) обеспечивает нулевой средний квадрат ошибки. Эти свойства легко устанавливаются из проведённого выше рассмотрения.

Процедура Грама-Шмпдта. Теперь предположим, что мы имеем ансамбль сигналов с ограниченной энергией (лД/), / -1,2,... Л/}, и хотим сконструировать ансамбль ортонормированных сигналов. Процедура ортонормирования Грама-Шмидта позволяет нам сконструировать такой ансамбль. Начнем с первого сигнала 5, (/), причём предполагается, что он имеет энергию <f,. Первый сигнал ортонормироаанного ансамбля конструируется легко:

/ДО. (4.2.32)

Таким образом, сигнал /ДО имеет форму s{t), но нормирован к единичной энергии. Второй сигнал конструируется из sil), причём сначала вычисляется проекция 5,(/) на Ait): .

с. [s,{t)f,{t)dt. (4.2.33)

Затем с,2/Д/) вычитается из s,{t) для получения

fAt) = s,{t)-c,2Ai(). (4.2.34)

Этот сигнал ортогонален /ДО, но не имеет единичной энергии. Если означает

энергию для / (/), то нормированный сигнал, который ортогонален к /ДО, равен

= (4.2.35)

В общем, ортогонализация к-й функции ведёт к

/.W = , (4.2.36)

1с-\

(0 = *(0-Ес„/(0 (4.2.37)

s,{t)fXt)dt, / = 1.2,...,А-1. (4.2.38)

Таким образом, процесс ортогонализации продолжается, пока все А/ сигналов не исчерпаны и не образованы N < М ортонормированных сигналов. Размерность N -сигнального пространства равна М, если исходные сигналы ансамбля линейно независимы, т.е. ни один из сигналов не является линейной комбинацией других сигналов.

Пример 4.2.2. Применим процедуру Грама-Шмидта к ансамблю четырёх сигналов, показанных на рис. 4.2.1(a). Сигнал s{t) имеет энергию , =2, так что /,(/) = лДл, (/). Далее мы видим, что с,, = 0; следовательно, s2{t) и /,(/) ортогональны. Как следствие, =sj{t)I-j¥k s-,{t). Чтобы получить /з(0, вычислим с,з и Сзз, которые равны

cf.-yfl и = О . Таким образом.

Поскольку /з (О имеет единичную энергию, то следует, что /з(/) - /, (/). Для определения /,(/) находим, что с,4 = , - О и с-4 = 1. Поэтому

/4W = 4W + V2/,(/)-/3(/) = 0.

Как следствие, 54(0 является линейной комбинацией /,(/) и /,(/) и поэтому /,(/) = О. Три ортонормированные функции показаны на рис. 4.2.1(b).

Поскольку мы сконструировали ансамбль ортонормированных сигналов {/,(/)}, можем

выразить М сигналов {5„(/) как линейную комбинацию от /,(/)} Таким образом, можно написать

А ,(0

Ч\/2

-1 г

/4(0=0

Рис. 4.2.1. Ортогонализаиия Грама-Шмидта для сигналов {s{l). (=i, 2, 3 {а) и соответствующие ортогональные сигналы (6)

*W = I!A„/,W, к = \,2,...,М,

(4.2.39)

<k-

11=1

(4.2.40)

Основываясь на выражении (4.2.39), каждый сигнал можно представить вектором

-[„.у,, ...i-,]. (4.2.41)

или, что эквивалентно, точкой в -мерном пространстве сигналов с координатами [s,, i = 1,2,...му. Энергия Аг-го сигнала равна квадрату длины вектора или, что эквивалентно, квадрату евклидова расстояния от начала координат к точке -мерного пространства. Таким образом, любой сигнал можно представить геометрически как точку в пространстве сигналов, заданном ортонормированными функциями.

Пример 4.2.3. Получим векторное представление четырех сигналов, показанных на рис. 4.2.1(a), используя ортонормальный ансамбль функций из рис. 4.2.1(6).

Поскольку размерность пространства сигналов N = 3, каждый сигнал описывается

тремя компонентами. Сигнал s(t) характеризуется вектором S=(V2,0,o). Аналогично

сигналы 5,(/), s{t), sit) характеризуются соответственно векторами S2=(o,V2,o),

S, =(V2,0,l), =(-л/2.0,l). Эти векторы показаны на рис. 4.2.2. Их длины равны

S =V2, js, =л/2, s3 =7з, is4j = -v3, а соответствующие энергии сигналов rf.-sj, = 1,2,3,4.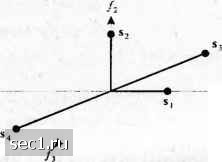

Рис. 4.2.2. Четыре сигнальных вектора, представленных в виде точек в трехмерном функциональном пространстве

Мы показали, что ансамбль М сигналов с ограниченной энергией можно представить взвешенной линейной комбинацией ортонормированных функций {/,(/)) размерностью М<М. Функции {/,(/)} получены применением процедуры ортонормализации Грама-Шмидта из .У„(0} Следует подчеркнуть, что функции {/,(0 , полученные преобразованием Грама-Шмидта, не являются уникальными (единственными). Если мы изменим порядок формирования ортонормированных сигналов из {s„U) > получим другой ортонормированный ансамбль и соответствующее векторное представление сигналов 5„(/)} будет зависеть от выбора ортонормальных функций {/,(0 Все же, вектора {s„