т + п = log M М-, двоичных символов, возникающих со скоростью К/{т + п). Примеры сигнальных пространственных диаграмм для комбинированной АМ-МФ показаны на рис. 4.3.4 для М-8 и М=1б.

Как в случае AM сигналов, КАМ сигналы можно представить как линейную комбинацию двух ортонормированных сигналов /,(/) и /2(/),т.е.

\,it) = \,M + s,Ml), (4.3.21)

Л/=8

Л/=16

Рис. 4.3.4. Примеры пространственных диаграмм для комбинированной АМ-ФМ

Ш = , -g[t)cos2nfj, ig{t)sm2Kfj

"•ml

(4.3.22)

(4.3.23)

Расстояние Евклида между произвольной парой сигнальных вектрров равно

Г4.3.24)

Для частного случая, когда амплитуда сигналов принимает ряд дискретных значений

\{2т-1- M)d, т\,2,---,М\, пространственная диаграмма сигналов является

прямоугольной, как показано на рис. 4.3.5.

В этом случае минимальное расстояние Евклида (между смежными точками) равно

d!i=d, (4.3.25)

что является тем же результатом, что для AM.

Многомерные сигналы. Из вышесказанного очевидно, что цифровая модуляция несущей по амплитуде и фазе позволяет конструировать сигналы, которые соответствуют двухмерным векторам и пространственным диаграммам сигналов. Если мы хотим сконструировать сигнал, соответствующий вектору большей размерности, можем использовать или временную, или частотную, или обе области для того, чтобы увеличить размерность пространства.

Предположим, что мы имеем -мерные сигнальные векторы. Для любого N можем разделить интервал времени длины T = NT на подынтервалов длиной T=TJN. В каждом интервале длины Т можем использовать двоичную AM (одномерный сигнал), чтобы передать элемент .V -мерного сигнального вектора. Таким образом. Л" временных отрезков используется для передачи Л -мерного сигнального вектора.

Рис. 4.3.5. Несколько пространственных диаграмм для прямоугольной КАМ

Если четно, отрезок длиной Г можно использовать для мгновенной передачи двух компонент -мерного вектора путем независимой модуляции амплитуды квадратурных несущих соответствующими компонентами. Таким путем iV-мерный сигнальный вектор передается за 7 Г секунд (у временных отрезков).

Альтернативно полоса частот ЛА / может быть подразделена на частотных отрезков, каждый шириной Д /. iV-мерный сигнальный вектор можно передать через канал путем одновременной (параллельной) модуляции амплитуды N несущих, одна на каждый из частотных отрезков. Надо позаботиться о достаточном частотном разносе А / между смежными несущими с тем, чтобы не возникала взаимная интерференция между сигналами ьа несущих. Если используются квадратурные несущие на каждом частотном отрезке, то -мерный вектор (- четно) можно передать па частотных отрезках, что

сокращает используемую каналом полосу частот вдвое.

В более общем виде мы можем использовать совместно временную и частотную области для передачи -мерного сигнального вектора. Например, рис. 4.3.6 иллюстрирует разделение частотно-временной области на 12 ячеек. Таким образом, можно передать jV=12-мерный сигнальный вектор при AM или Л=24-мерный сигнальный вектор с использованием двух квадратурных несущих (КАМ) на кавдом отрезке.

/+4Д/ /+ЗД/ /+2Д/ /+А/

2т 37-

Рис. 4.3.6. Разделение осей времени и частоты на индивидуальные отрезки

Ортогональные многомерные сигналы. Как специальный случай конструирования многомерных сигналов с нелинейной модуляцией рассмотрим случай конструирования М ортогональных сигналов равной энергии, которые различаются по частоте и представлены как

s,„it) = Re [s. „(/) е- J = д со42л ft + 2nmAft m = l,2,...,M, 0</<Г, где эквивалентный низкочастотный сигнал определяется так:

л„(0 = л)е-"-, т = \,2,-.М, Q<t<T.

(4.3.26)

(4.3.27)

Этот вид частотной модуляции (ЧМ) называется модуляцией иаспютиым сдвигом (M4C,FSK).

Эти формы сигналов характеризуются равной энергией и коэффициентами взаимной корреляции

2т; г- ,,,(,„.,)др 5шяГ(;7г-)Д/ ,,(,„ ,)д, Вещественная часть р.,„ равна

(4.3.28)

(\ sm Kill - IK 11Л I г , . 1 am Z.JI.1 кт - п, i la /

1п-п-.)А/ Ч"Пш-.)А/]= I. (4.3.29)

Сначала заметим, что Re(p4,„) = 0, когда А/= 1/(2Г) и тФк. Поскольку случай т-к\ = \ соответствует соседним частотным интервалам, то Д/ -1/{2Т) представляет .минимальную величину частотного разноса между смежными сигналами для ортогональности М сигналов. Кривые зависимости Ке(р.,„) от А/ и р„; от А/

показаны на рис. 4.3.7. Заметим также, что р,„, =0, если А/ кратно в то время как

Re(p;,„) = 0. когда А/ кратно 1/(2Г).

TiT{m-k)Af

2TiT[m-k)Af

IP.,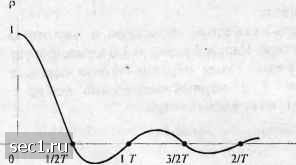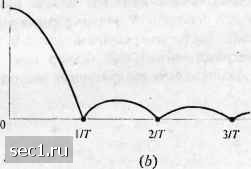

Д/"

Рис. 4.3.7. Коэффициент взаимной корреляции как функция от частотного разноса для сигналов МЧС

Для случая, когда А/ = 1/(2Г), ансамбль из М сигналов МЧС эквивалентен Af-мерным векторам