Р-ЕД., (4.3.47)

где, = р(йг,=0)ид,=р(а,=1).

Для сигнала NRZI с равновероятными состояниями Pi=P2 = 2 матриц перехода, определяемых (4.3.42) и (4.3.42), матрица переходных вероятностей равна

± 1

(4.3.48)

Аналогично матрица переходных вероятностей для сигналов, кодированных по Миллеру, при равновероятных символах (£/=(72=Т> *""о эквивалентно,

Р>= Pi Р.= P4=i) равна

±

±

±

±

(4.3.49)

Матрица переходных вероятностей используется при определении спектральных характеристик техники цифровой модуляции с памятью, как мы покажем в разд. 4.4.

4.3.3. Нелинейные методы модуляции с памятью ,

В этом разделе мы рассмотрим класс методов цифровой .модуляции, в которых фаза сигнала поддерживается непрерывной. Такая поддержка приводит к модуляции по фазе или по частоте с памятью. Метод модуляции нелинеен.

Частотная модуляция с непрерывной фазой (ЧМНФ). Обычный сигнал ЧМ или модуляции с частотным сдвигом (МЧС или FSK) генерируется путём сдвига частоты несущей на величину f„=-rAfI„, /„ = ±1,±3,...,±(Л/-1), чтобы отразить цифровую информацию, которую надо передать. Этот вид модуляции сигналов был описан в разделе 4.3.1 и он без памяти. Переход от одной частоты к другой может быть выполнен посредством М = 2* отдельных генераторов, настроенных на необходимые частоты, и выбора одной из М частот согласно частному значению Л-битового символа (б;юка), который должен быть передан на сигнальном интервале длиной Т - k/R секунд.

Однако такое резкое переключение с выхода одного генератора на выход другого в смежных сигнальных интервалах, приводит к относительно большим долям боковых частотных составляющих вне основной спектральной полосы сигнала, и, следовательно, этот метод требует большую полосу частот для передачи сигнала. Чтобы избежать использования сигналов с большими долями боковых полос, информационный сигнал может модулировать одну несущую, частота которая меняется непрерывно. Результирующий частотно-модулированный сигнал имеет в этом случае непрерывную фазу и поэтому назван ЧМ с непрерывной фазой (ЧМНФ, CPFSK). Этот вид ЧМ сигнала имеет память, обусловленную тем, что фазу несущей заставляют быть непрерывной.

Чтобы представить сигнал ЧМНФ, мы начнём с сигнала AM

dit) = Zl„g{t-nT), (4.3.50)

где {/,,} означает последовательность амплитуд, полученную путём отображения к -битовых блоков двоичных символов от информационных последовательностей [а] в уровни амплитуды ±1,±3,...,±(М-1). - прямоугольный импульс с амплитудой 1/2Г и

длительностью Г секунд. Сигнал d{t) используется для частотной модуляции несущей. Следовательно, эквивалентный низкочастотный сигнал V){t) можно в этом случае выразить так:

(4.3.51)

где максимальная девиация частоты, а фд-начальная фаза несущей. Частотно-модулированный сигнал, соответствующий (4.3.51), можно выразить как

s{t) =

2я/:./ + ф(/;1)-ьф,

где ф(/;1) представляет меняющуюся во времени фазу несущей:

Ф(/;1) = 4717ГЛ d{x)dx4nTf,

(4.3.52)

(4.3.53)

Заметим, что d{t) содержит разрывы, интеграл же от dit) непрерывен. Следовательно, мы имеем сигнал с непрерывной фазой. Фаза несущей на интервале nT<t<{п + \)Т определяется интегрированием (4.3.53) таким образом:

ф(г; I) 2nfJ S 4 + 2л/л( - пТ)1„ = е„ + 2nhl„q {t - nf),

где /г, 9„ и q{t) определяются так:

Й-2ЛГ,

(4.3.54J

(4.3.55) (4.3.56)

(/<0),

q{t)=\tl2T {0<t<T), (4.3.57)

i и>т).

Видим, что 9„ представляет накопление (память) от всех информационных символов, переданных до момента {п-\)Т. Параметр h называется индексом модуляции.

Модуляция с непрерывной фазой (МНФ). Выраженный в виде (4.3.54) сигнал ЧМНФ является специальным случаем общего класса сигналов МНФ (модуляции с непрерывной фазой), в которой фаза несущей определяется так:

.1-1

ф(г;1) = 271 YhKQil-T), nT<t<{n + l)T,

(4.3.58)

к W

где {/j}-последовательность информационных символов, выбранных из алфавита ±1,±3,...,±(М-1), {\}-последовательность индексов модуляции, а ql/)-нормированная огибающая сигнала.

Когда h=h для всех к, индекс модуляции фиксирован для всех символов. Когда индекс модуляции меняется от одного символа к другому, сигнал МНФ называется многоиндексным (multi-h). В этом случае [h,] меняется циклически, принимая значения ряда индексов. Форму сигнала q{t) можно представить в общем виде как интеграл от импульса g{t):

q{t)-lg{x)dz.

(4.3.59)

Если g(/) = 0 для t>T, сигнал МНФ называют МНФ с полным откликом. Если Ф)фО для t>T, модулированный сигнал называют МНФ с частичным (парциальным) откликом. Рисунок 4.3.16 иллюстрирует несколько форм огибающих импульсов g{/) и соответствующих форм q{i). Очевидно, что неограниченное число разновидностей сигналов МНФ можно генерировать выбором различных огибающих импульсов g(/) и изменением индекса модуляции h и размера алфавита М.

1/(27)

t г(0(1-со5(2л Г))/27

1/(4Г)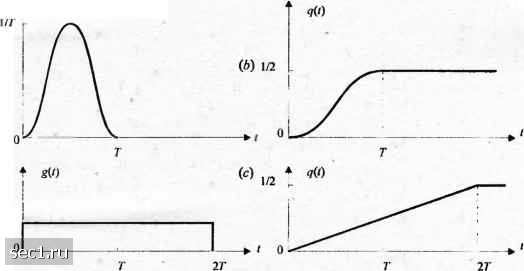

" й(0=(1-со5(л Г))/4Г

1/(27)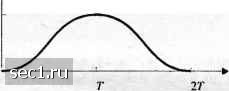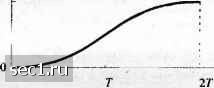

Рис. 4.3.16. Формы импулы:ов для полного агклика МНФ (а. а) и для парциального отклика МНФ (с, d)

Поучительно нарисовать ряд фазовых траекторий ф(/;1), генерируемых возможными

значениями информационных последовательностей Например, для случая ЧМНФ с

двоичными символами /„ = ±1 и прямоугольным импульсом ряд фазовых траекторий, начинающихся при времени / = 0, показан на рис. 4.3.17. Для сравнения фазовые траектории для четырёхпозиционной ЧМНФ иллюстрируются на рис. 4.3.18. Эти фазовые диафаммы называют фазовым деревом. Видим, что фазовые деревья для ЧМНФ являются кусочно-линейными, как соадствие того факта, что импульс g(t) прямоугольный. Гладкие