фазовые траектории и фазовые деревья получены также при использовании импульсов, которые не имеют разрывов, таких как класс импульсов приподнятого косинуса. Для

примера фазовая траектория, генерируемая последовательностью 1,-1, 1, 1,-1, l),

при парциальном отклике импульса приподнятого косинуса длины ЗГ иллюстрируется на рис. 4.3.19. Для сравнения показаны соответствующие фазовые траектории, генерируемые при ЧМНФ.

5hn - - . •

41т . . - . - .

+ 1 -1

21т . - , •

+1 -1 +1

21т ----- . . ----- . . -.

+1 -I +1-1

/т----------- .. - --- . - - ------ -ф

+ 1 -1 -t-l -I +1

О .. . , . .

-1 +1 -1 +1 -1

-Ал . - . ------ -ф . ------- -

; -1 +1 -I +1,/ : ; -1 +1 -1

-31т • ... ,

-I +1

-41т • ----, . --- ------.

: , -1

-ЗЛтг--------1 -----1- - л - - ->------0

Т 2Т ЗТ 4Т 5Т

Рис. 4.3.17. Фазовые траектории для двоичной ЧМНФ

Фазовые деревья, показанные на этих рисунках, растут со временем. Однако фаза несущей однозначна только в области от ф = О до ф - 2я или, что эквивалентно, от ф = -я

до ф = я. Если фазовые траектории определить по модулю 2л, скажем в области (-я,я),

фазовое дерево превратится в структуру, называемую фазовой решёткой. Для надлежащего обозрения диаграмм фазовых решёток можем строить две квадратурные компоненты .Y (/;l) = созф(/;1) и х,(/;1) = зшф(/;1) как функции времени. Таким образом, мы генерируем трёхмерный график, в котором квадратурные компоненты и возникают на поверхности цилиндра единичного радиуса. Например, рис. 4.3.20 иллюстрирует фазовую решётку или фазовый цилиндр, получающийся при двоичной модуляции с индексом модуляции А = 4 и использовании импульса принятого косинуса длиной ЗТ.

Простое представление фазовых траекторий можно получить, показывая только финальные значения фаз сигнала в моменты времени i = пТ. В этом случае мы ограничиваем индекс модуляции сигнала МНФ рациональными значениями. В частности, предположим, что h = mlp, где тпр-взаимно простые целые числа. ТогдаМНФ-сигнал с полным откликом в моменты времени t -пТ будет иметь финальные состояния

3/1л

2/l7t

-2*л

-ЗЛл

-4Лл

-51т

-6Ал L

"+1

Т IT ът

Рис. 4.3.18. Фазовые трае1сгории для четырёхпозиционной ЧМНФ

, t ФУ.»

2ЛЛ L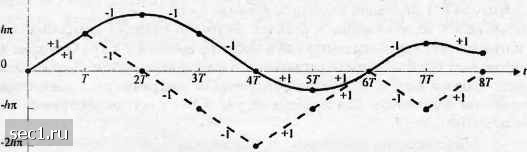

Рнс. 4.3.19. Фазовые траектории для двоичной ЧМНФ (штриховой линией)) и двоичной МНФ с парциальным откликом, основанным на импульсе приподнятого косинуса длительностью ЪТ [Sundberg (1986). © 1986 1ЕЕЁ\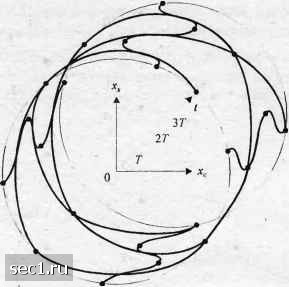

Рис. 4.3.20. Фазовый цилиндр для двоичной МНФ с Л = 1/2 и с импульсом приподнятого косинуса длительностью ЗГ [Sundberg (1986), © 1986 /ЕЕЕ]

(л In ™. 12™.

когда т - четно, и

0: =

<л ГШ 2 ты

р 3 р 5 •••5 р

(4.3.60)

(4.3.61)

когда т - нечётно. Следовательно, имеется р финальных состояний фазы, когда т - четно, и 2р состояний, когда т - нечётно. С другой стороны, когда огибающая импульса простирается на L символьных интервалах (МНФ с парциальным откликом), число состояний фазы может увеличиваться до максимального значения 5,, где

(jn чётное).

rl-\

(4.3.62)

\2рМ (jfj нечётное), где М - объём алфавита. Например, двоичная ЧМНФ (полный отклик, прямоугольный импульс) с h-\ имеет S. = 4 финальных фазовых состояний. Решётка состояний для этого сигнала показана на рис. 4.3.21. Подчеркнём, что переход фазы из одного состояния в другое не затрагивает промежуточные фазовые траектории. Они здесь представляют фазовые переходы для состояний в моменты времени t -пТ.

Альтернативной по отношению к решётке состояний является диаграмма состояний, которая иллюстрирует переходы состояний в моменты времени t = пТ. Она даже является более компактным представлением сигнальных характеристик МНФ. Только возможные финальные состояния фазы и их переходы отражены на диаграмме состояний. Время здесь не выступает как переменная. Для примера на рис. 4.3.22 показана диаграмма состояний для сигнала ЧМНФ с h=l/2.

Модуляция с минимальным сдвигом (ММС, MSK). ММС - специальная форма двоичной ЧМНФ (и, следовательно, МНФ), в которой индекс модуляции /г = у. Фаза несущей на интервале nT<t<{n + l)T равна