ф,=37г/2

ф,=л/2 9

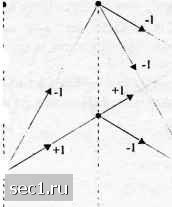О 7" 27 ЗГ 4т

Рис. 4.3.21. Решетка состояний для двоичной ЧМНФ с А=1/2

-1 +1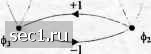

Рис. 4.3.22. Диаграмма состояний для двоичной ЧМНФ с Л=1/2

t-пТ

у Т J

nT<t<{n + l)T,

а сигнал модулированной несущей равен

s(t) = А cos

= у4 cos 2л

nTt<{n + \)T.

(4.3.63)

(4.3.64)

Формула (4.3.64) указывает на то, что сигаал двоичной ЧМНФ может быть выражен как синусоида, имеющая одно из двух возможных значений частоты на интервале nT<t <{п + \)Т. Если мы определим эти частоты так:

(4.3.65)

тогда сигнал двоичной ЧМНФ, определяемый (4.3.64), можно записать в виде

5,(/) = Aco2nfX + Q„ +imr(-1)"], i = 1, 2. (4.3.66)

Разность частот А/" =/j -/, = 1/2Г. Напомним, что А/" = 1/27- это минимальная разность частот, необходимая для обеспечения ортогональности сигналов s{t) и .SjlO на

сигнальном интервале длиной Т. Это объясняет, почему двоичную МНФ с h-j называют модуляцией с минимальным сдвигом (ММС). Фаза на п-м сигнальном интервале определяется состоянием фазы сигнала, которая образуется для непрерывности фазы между соседними интервалами.

ММС можно таклсе представить как разновидность четырёхфазного ФМ. Конкретно мы молсем выразить эквивалентный низкочастотный модулирующий сигнал в виде

it) = JlUb.git - 2пТ) - j I,„,g(t - 2пТ-Т)

(4.3.67)

где gft)

(4.3.68)

сигнальный импульс, определяемый так:

fsinff (0</<2Г), [о (для других/).

/ Таким образом, этот тип сигнала можно рассматривать, как четырёхпозиционный сигнал ФМ, в котором огибающая импульса является полупериодом синусоиды. Чётные

двоичные (+1) символы Д,,} от информационной последовательности /„ передаются

при помощи косинусоиды несущей, в то время как нечётные двоичные (±1) символы {Д„+}" передаются при помощи синусоиды "несущей. Скорость -передачи двух ортогональных несущих равна 1/2Г бит/с, так что суммарная скорость передачи равна 1/Г бит/с. Заметим, что битовые переходы на синусной и косинусной несущей смещены во времени на Т секунд. Из этих соображений сигнал

s{t) = A<

Y.Ii,dt-2nT) cos2nfJ

X4,,,g(/-2nr-r)

sin2nfj

(4.3.69)

называют офсетной квадратурной ФМ (ОКФМ, OQPSK) или квадратурной ФМ со сдвигом (КФМС, SQPSK).

Рисунок 4.3.23 иллюстрирует представление ММС-сигналов как двух смещённых квадратурно-модулированных двоичных ФМ-сигналов. Сумма двух квадратурных сигналов является частотно-модулированным сигналом с постоянной амплитудой.

Интересно сравнить форму сигнала ММС с ОКФМ, в котором импульс g{t) является прямоугольным на интервале (0<t<2Т), с обычной квадратурной ФМ (КФМ), в которой импульс g{t) также прямоугольный на интервале (О < / < 2Г). Ясно, что все три метода дюдуляции работают при одинаковой скорости передачи данных. ММС сигнал имеет непрерывную фазу. ОКФМ-сигнал с прямоугольным импульсом принципиально является суммой двух двоичных ФМ-сигналов, в которых переходы фазы возникают через Т секунд. Таким образом, сигнал имеет скачки фазы на + 90", которые могут возникнуть не чаще, чем через Т секунд. С другой стороны, обычная четырёхпозиционная ФМ с постоянной амплитудой может иметь скачки фазы ±180° или ±90° каждые 2 Г секунд. Иллюстрация этих трёх типов сигналов дана на рис. 4.3.24.

Пространственные диаграммы для сигналов МНФ. В общем, сигналы с непрерывной фазой не могут быть представлены в дискретных точках в пространстве сигналов, как в случае AM, ФМ и КАМ. поскольку фаза несущей меняется во времени. Вместо этого сигнал с непрерывной фазой описывается переменными фазами или траекториями перехода от одного состояния фазы к другому.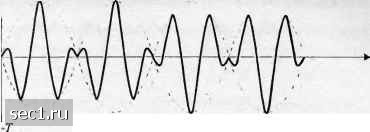

Т 37 5Т IT

(а) Синфазная сигнальная компонента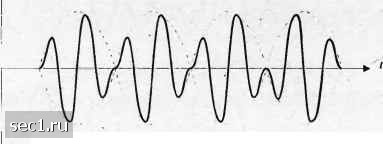

О 2Т 4Т 6Т

(Ь) Квадратурная сигнальная компонента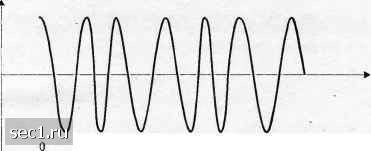

Т 2Т ЗТ 47" 57 6Т (с) Сигнал ММС [сумма (а) и (6)]

Рис. 4.3.23. Представление сигнала ММС суммой двух взаимно

сдвинутых сигналов ФМ, каждый с синусоидальной огибающей

Для сигналов МНФ с постоянной амплитудой переменные траектории образуют окружность. Для примера на рис. 4.3.25 иллюстрируется диаграмма пространства сигналов (фазовые траектории) для МНФ с h = \, h = \, h = \, Л =

Места начала и конца этих фазовых траекторий отмечены на рисунке точкой. Заметим, что длина фазовой траектории увеличивается с ростом h. Рост h ведёт также к расширению полосы частот, как будет показано в следующем разделе.

.Многоуровневая МНФ. Многоуровневая МНФ является обобщением обычной МНФ. в которой амплитуда сигнала может принять ряд значений, в то время как фаза поддерживается непрерывной. Для примера рассмотрим двухуровневый сигнал ЧМНФ, который можно представить так:

t)=2A co\2nfj + ф J (/; l)] + А со\2ф + ф, j)

, , Khl(t-nT) , ,

ф,(/;1) = лЛ24+- иГ</<(л + 1)Г,

(4.3.70)

(4.3.71)