сдциг фазы -90 сдвиг ()азы +90

(а) ММС

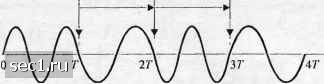сдвиг фазы -90 сдви! фазы +90

сдвиг фазы 90

(6) о(1)сетная квадратурная ФМ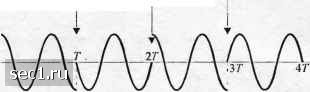

сдвиг фазы 180

у пет перемены данных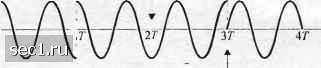

(с) квадратурная ФМ

сдвиг фазы -90

Рис. 4.3.24. Сигнал для (а) ММС, (Ь) офсетной квадратурной ФМ (прямоугольный импульс) .и (с) обычной квадратурной ФМ (прямоугольный импульс) [Gronemeyer и McBride (1976); © \ Ш IEEE]

/;=1 4

А-1/3

А=1/2

/7=2/3

Рис. 4.3.25. Пространственная диаграмма сигнала ЧМНФ iihJ,Xt-nT)

пГ<1<{п + \)Т.

(4.3.72)

. Информация передаётся последовательностями символов {/„} и {J,J , которые связаны с двумя независимыми двоичными информационными последовательностями {а,,) и {6„), принимающими значение {0,1}. Видим, что сигнал в (4.3.70) является суперпозицией двух сигналов ЧМНФ с различными амплитудами.

Для детальной проработки рассмотрим случай, когда /2-7, так что .мы имеем суперпозицию двух ММС-сигналов. В точке передачи компоненты с различными амплитудами находятся либо в фазе, либо в противофазе. Изменение фазы сигната определяется фазой компоненты с большой амплитудой, в то время как изменение амплитуды определяется компонентой с меньшей амплитудой. Поэтому меньшая компонента управляется так, чтобы в начале и в конце символьного интервала, она находилась в фазе или была сдвинута на Г80° относительно компоненты с большой

амплитудой, независимо от фазы последней. При таком управлении последовательности символов {/„} и {J,} можно вьфазить так:

Эти соотношения отражены в табл. 4.3.1.

(4.3.73)

Как обобщение, сигнал многоуровневой ЧМНФ с п компонентами можно выразить так:

j» -1

sit) 2- co{2nfj-ьфД/;l)] + Х"" cos[2</ + ф,Д; J,„)

11-1

фд,(/;1) = яМ„- + тг/гХ/*, nT<t<{n + \)T,

Ф,„(;Л,„) = Ля[/г+(л„+1)

t пТ

i;-l

+ E4[ + tU.*+i)1, nT<t<[n + \)T.

к- «.

(4.3.74)

(4.3.75)

(4.3.76)

Последовательности {/„} и {J,,,,,} статистически независимы, они двоичные, а символы принимают значения из ряда {1, -1} .

Из (4.3.75) и (4.3.76) видим, что каждая компонента в сумме будет или в фазе, или со сдвигом 180° относительно фазы наибольшей компоненты в концах интервала п-го символа, т.е. при t - {п + \)Т. Таким образом, состояния сигналов определяются уровнями

амплитуд из ряда значений l, 3,5,...,2-1} и значениями фаз из ряда

О, я9,2т19....,2т1-я/7}. Управление фазой требуется для того, чтобы поддерживать

непрерывной фазу сигнала МНФ.

Рисунок 4.3 26 иллюстрирует диаграмму состояний сигнала для двухамплитудной (л =2) ЧМНФ с /г = 7.у,у и у. Диаграммы состояний трёхкомпонентиой (М = 3) ЧМНФ показаны на рис. 4.3.27. В этом случае имеются четыре уровня амплитуд. Число состояний зависит как от индекса модуляции h, как и от N. Дополнительные многоуровневые формы сигналов ЧМНФ можно получить с использованием как огибающих импульсов, отличных от прямоугольных, так и сигнальных импульсов, которые тянутся более чем на интервал одного символа (парциальный отклик).

/1-1/2

-2 A1-1

0 112

,3 -3

ii-m

Рис. 4.3.26. Пространственная диаграмма сигнала двухкомпонентной ЧМНФ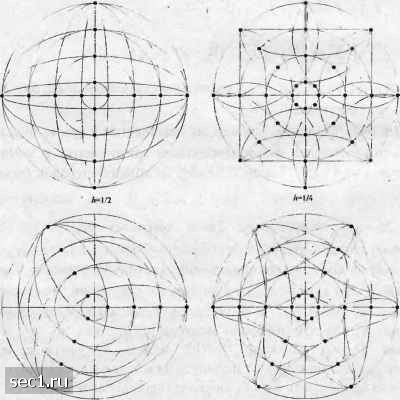

л-1/3

Рис. 4.3.27. Пространственная диаграмма сигнала трёхкомпонентной ЧМНФ