компоненты исчезают, когда информационные символы имеют нулевое среднее, т.е. ц, = О. Это условие обычно желательно для техники цифровой модуляции. Оно выполняется, когда информационные символы равновероятны и симметрично расположены на комплексной плоскости. Таким образом, проектировщик системы может управлять спектральными характеристиками сигналов цифровой модуляции путём специального подбора характеристик информационной последовательности, которую нужно передать.

Пример 4.4.1. Чтобы проиллюстрировать влияние g{t) на огибающую спектра, рассмотрим прямоугольный импульс, показанный на рис. 4.4.1(a). Преобразование Фурье от g{l) равно

Wsin л /" Г ,... -AT е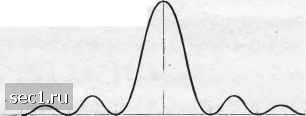

О Т -3/т -2it л г О 1 Г ит 3jt

{а) Ф)

Рис. 4.4.1. Прямоугольный импульс и его спектральная плотность энергии \G(J)\-Следовательно,

sin Л / Т

(4.4.19)

1. п/Т J

Этот спектр показан на рис. 4.4.1(6). Заметим, что спектральная плотность принимает нулевые значения в точках оси частот, кратных 1/Г, и убывает обратно квадрату частоты.

Как следствие наличия нулей в все дискретные спектральные компоненты в (4.4.18),

кроме одной, исчезают. Подставляя (4.4.19) в (4.4.18), имеем

зшл /г

V?s(/).

(4.4.20)

Пример 4.4.2. В качестве второй иллюстрации влияния на огибающую спектра импульса g(/) рассмотрим импульс приподнятого косинуса

0<t<T.

(4.4.21)

График этой функции дан на рис. 4.4.2(<7). Его преобразование Фурье легко получить, и его можно выразить в виде

«(/)=

AT sin л/Г

(4.4.22)

2 nfr{l-fr-)

Квадрат амплитуды g(/) показан на рис. 4.4.2(6). Интересно отметить, что спектр имеет нули в точках f = n/T, п-±2, ±3, ±4,.... Следовательно, все дискретные

спектральные компоненты в (4.4.18), кроме тех, которые на частотах /-Он / = ±1/Т, исчезают. По сравнению со спектром при прямоугольном импульсе спектр приподнятого косинуса имеет более широкий главный лепесток, но хвосты уменьшаются обратно .

\G(f)\

s(.i)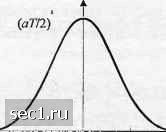

-4/Г -3/7- -2/Т -\1Т О

1/7-

3/Т 4/Г

Рис. 4.4.2. Импульс приподнятого косинуса и его спектральная плотность энергии \G(f)\

Пример 4.4.3. Чтобы проиллюстрировать влияние на огибающую спектра операций, выполняемых по отношению к информационной последовательности, рассмотрим двоичную последовательность {6,,}, по которой формируем символы информационной последовательности

/.=6„+6„ ,. (4.4.23)

Предполагается, что последовательность {6, } содержит некоррелированные случайные величины, каждое с нулевым средним и единичной дисперсией. Тогда автокорреляционная функция последовательности {/„} равна

2 т = 0.

ф,Дт) = £(4/ ,) =

(4.4.24)

1 ш = ±1, О другие т.

Следовательно спектральная плотность мощности входной последовательности равна

Ф,(/) = 2(1 + соз2л/г) = 4соз7г/Г, (4.4.25)

и соответствующая спектральная плотность мощности для (низкочастотного) модулирующего сигнала

.if)=rHffoosKfT.

(4.4.26)

4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ

В этом разделе мы получим спектральную плотность мощности для класса сигналов МНФ с постоянной амплитудой, которые были описаны в разд. 4.3.3. Начнём с расчёта автокорреляционной функции и её преобразования Фурье, как мы это сделали в случае линейной модуляции. Сигнал МНФ с постоянной амплитудой выражается так:

s{t; l) = A coJlnfj + ф(/; l) if{t;l) = 2nhfI,q{t.-kT)

(4.4.27)

(4.4.28)

Каждый символ последовательности {/„} может принять одно из М значений {±1,±3,...,+(М-1). Эти символы статистически независимы и одинаково распределены с априорными вероятностями

i, = p(/,=4 « = ±1,±2,...,±(M-1). (4.4.29)

Импульс /) = dq{t)Idt равен нулю вне интервала О, LT , q{t) = О, t <0 и q{t) - j для t> LT. Автокорреляционная функция эквивалентного низкочастотного сигнала о(/) = е*- равна

j2nhY,l\q{t + x-kT) qit-кТ)

(4.4.30)

Сначала выразим сумму в показателе экспоненты как произведение экспонент. Результат равен

YI ехр{ jlnhl, [q{t + T-kT)-q{t-- кТ)

*=-00

(4.4.31)

Далее найдём математическое ожидание по символам {/} . Поскольку эти символы

статистически независимы, получаем

Ф.о( + с;0 = тП E«exp{7m«[g(/ + T-/tr)-g(r- /tr)

п нечетные

Наконец, усреднённая во времени автокорреляционная функция равна

Ф»=-Гфи.{+;М-

(4.4.32)

(4.4.33)

Хотя (4.4.32) подразумевает, что имеется неограниченное число множителей, импульс g(t) = dqit)/dt = О для /<0 и t>LT, а q{t) = 0 для /<0. Как следствие, только ограниченное число слагаемых в произведении имеет ненулевые значения показателя экспоненты. Таким образом, (4.4.32) можно существенно упростить. Если принять T = t + mT, где 0<<Г и аи = 0, 1,то усреднённая автокорреляционная функция (4.4.33) приводится к результату

Т 1П+1

о k=\-L

П Е Р„ехр{у2яЦ(/ + -(-т)г)-(/-7)]}

V(, -(Д.-1) л нечешые

(4.4.34)

Рассмотрим \ \л-тТ) для \л-тТ>1.Т. В этом случае (4.4.34) можно выразить так:

фJ + mГ) = [ч/(7/г)fЛfe), m>L, 0<<Г, (4.4.35)

где \/(у/г) - характеристическая функция для случайной последовательности {/„}, определяется так:

(4.4.36)

n нечетные

a - остаточная часть усреднённой автокорреляционной функции, которую можно выразить как