() = Ш f Т.Рп ехр{727гЦ1 - git - кТ)

1 f М-\

П S. Qx[j2nhnq[t + -кТ]

A = 1-LV„:=-(M-1) я нечетные

(4.4.37)

dt, m>L.

Таким образом, J<x) можно представить произведением и степени как

указанно в (4.4.35) для т = + тТ > LT и 0<<Г. Эти свойства используются ниже.

Преобразование Фурье (т) даёт среднюю спектральную плотность мощности

Фии(/)= }ф»е-Л = 2Ке

ф(г)е-Л

jTh--dT= ]ф„г)е-Л+ jJxh-dx.

о о LT

С учётом (4.4.35) интеграл в области LT<x <со можно выразить так:

оо ОЭ (л1+1)

LT n=i тТ

Теперь пусть т = ч-отГ. Тогда (4.4.40) выражается как

(4.4.38)

(4.4.39)

(4.4.40)

ф„т)е--х = ± ]и + тТ)е--Ч =

и- "" о

Характеристическая функция удовлетворяет условию

которых 4/(7/?) < 1, сумма в (4.4.41) сходится к результату

В этом случае (4.4.41) приводит к виду

(4.4.41)

1/(УА) < 1. Для значений h, для (4.4.42)

Объединяя (4.4.38), (4.4.39) и (4.4.43), получаем формулу для спектральной плотности мощности сигнала МНФ в виде

lT (L+\)r

(4.4.44)

Ф..(/) -2Re К„(т)еЫх + j Ф..{т)е--т

Это требуемый результат, когда \i{j}ij<\. В общем, спектральная плотность мощности вычисляется численно по формуле (4.4.44). Усреднённую автокорреляционную функцию фуц(т) для области 0<t<(Z + l)r можно вычислять численно из (4.4.34). Для значений h, для которых ч/(ул) = 1, например h = К, где К - целое, можно положить

Ч/(ул)-е"\ 0<v<l. (4.4.45)

12* 179

Тогда сумма в (4.4.41) даёт

1,-0

Т Т.

-JjCtgnT\f-~ V 1.

(4.4.46)

Таким образом, спектральная плотность мощности теперь содержит дискретные компоненты, локализованные на частотах

и +V

0<v<l, 0 = 0,1,2,....

(4.4.47)

Результат (4.4.46) можно объединить с (4.4.41) и (4.4.39), чтобы получить полную спектральную плотность мощности, которая включает компоненту с непрерывным спектром и компоненту с дискретным спектром.

Вернёмся к случаю /(у/г) < 1. Если информационные символы равновероятны, т.е.

Л =-тт для всех п.

то характеристическая функция упрощается до выражения

/ ч 1 1 sinMn/2

11/(7/2) =

M„. t

(л/ 1) я нечетные

М зшлЛ

(4.4.48)

Заметим, что в этом случае Н(У) вещественно. Усреднённая автокорреляционная функция, определяемая (4.4.34), также упрощается в этом случае:

1 Г М 1 sin2яШ\q{tx-kT]-q{t-кТ)

Фоо(2г1,11 М sm2nh\qit + T-kT)-q{t-kTf

(4.4.49)

Соответствующее выражение для спектральной плотности мощности

Фио(/) = 2 ф>)со827г/тЛ +

i-Jjh) С052пД . f- , ,

+-\ / \ - I Ф (тсоз2я/Л

l + \l)(jh)-2\ii(jh)cos2Tifr .1 "

(4.4.50J

Спектральная плотность мощности для ЧМНФ. Замкнутое выражение для спектральной плотности мощности можно получить из (4.4.50) тогда, когда огибающая импульса g{t) прямоугольная и равна нулю вне интервала [0. Т]. В этом случае q{t) линейно для Q<t <Т. Результирующую спектральную плотность мощности можно выразить так:

г 1 М J М At

JfhT -1Д(/)+-;ЕХ5.,(/)л(/)Л,(/) , (4.4.51)

4,W:

Sin Я

fr-H2n-l- M)h

fr-\{2n-\-M)h

( Л о(2яуГ g,,,,) - 4/ cosa,, "" 1 + М/-2ч;со52я/Т

a,„„ = Tih{m + n-\~ M),

(4.4.52)

Спектральная плотность мощности ЧМНФ для Л/ = 2, 4 и 8 показана соответственно на рис. 4.4.3-4.4.5 как функция нормированной частоты / Т при индексе модуляции h = 2f, Т в качестве параметра. Заметим, что на графиках показана только половина занимаемой полосы частот. Начало координат соответствует частоте несущей /,.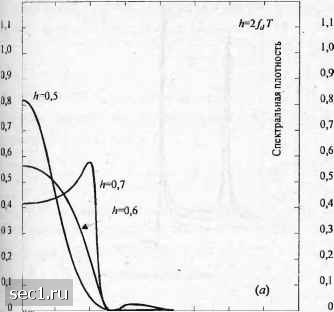

Нормированная частота /Г

0.4 0,8 1,2

Нормированная частота /7"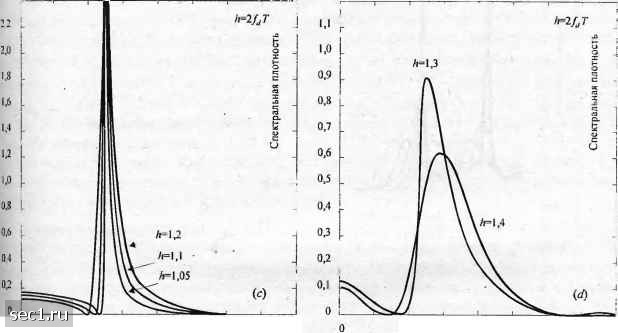

0,4 0,8 1,2

Нормированная частота /Т

0.4 0,8 1,2

Нормированная частота /7"

Рис. 4.4.3. Спектральная плотность мощности двоичной ЧМНФ

Графики показывают, что спектр ЧМНФ относительно узкий и хорошо ограничен при h<\. Когда h приближается к единице, в спектре отмечаются большие выбросы, и при h\, когда v/ = 1, мы находим, что пики возникают на М частотах. Когда h>\, спектр

получается значительно шире. В системах связи, в которых используется ЧМНФ. индекс .модуляции рассчитывается так, чтобы экономить полосу, так что h<\.