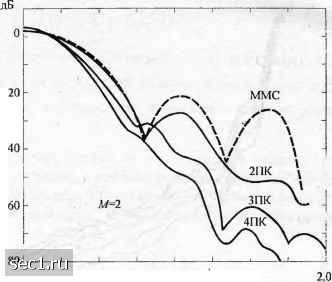0,5 1,0 1.5

Нормированная частота /7"

Рис. 4.4.8- Спектральная плотность мощности МНФ ch=\l2 и различной формой огибающей импульса [Aulin и др. (1981); © 1981 1ЕЕЕ\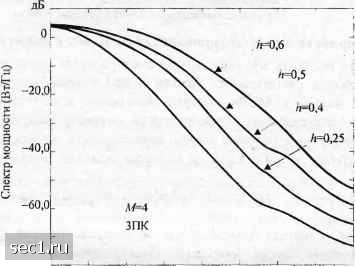

-80.0

0Д5 0,5 0,75

Нормированная частота fT

Рис. 4.4.9. Спектральная плотность мощности МНФ для М=4 с ЗПК и различными индексами модуляции {Avlin и др. (1981);© 1981 IEEE]

Влияние изменения индекса модуляции в сигнале МНФ иллюстрируется на рис. 4.4.9 для случая М = 4 и импульса приподнятого косинуса формы данной (4.4.56) с 1 = Ъ. Заметим, эти спектральные характеристики похожи на те, которые ранее иллюстрировались для ЧМНФ, за исключением того, что этот спектр уже из-за использования гладкой огибающей импульса.

Наконец, на рис. 4.4.10 мы иллюстрируем зависимость доли внеполосной мощности от нормированной частоты для двухамплитудной ЧМНФ с несколькими различными значениями h.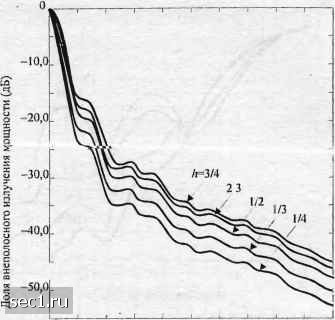

о 0Д5 0,50 0.75 1,00 1,25 1,50 1,75 2,00 2,25 2,50 Нормированная частота fT

Рис. 4.4.10. Относительная величина внеполосной мощности для двухкомпонентной ЧМНФ (Milligan, 1988)

4.4.3. Спектр мощности для модулированных сигналов с памятью

В двух последних разделах мы определили спектральные характеристики для класса линейно модулированных сигналов без памяти и для класса модулированных по фазе сигналов, таких как ЧМНФ и МНФ, которые нелинейны и обладают памятью. В этом разделе рассмотрим спектральные характеристики линейно модулированных сигналов: которые обладают памятью и которые можно моделировать марковской цепью. Мы уже встречали такие сигналы в разд. 4.3.2, в котором описали несколько типов базовых сигналов.

Спектральную плотность мощности цифрового модулирующего сигнала, который описывается цепью Маркова, можно получить при помощи базовой процедуры, данной в предыдущих разделах. Сначала определяется автокорреляционная функция, а затем с помощью преобразования Фурье находится спектральная плотность мощности. Для сигналов, которые описываются цепью Маркова с матрицей переходных вероятностей Р, спектральную плотность мощности сигнала можно выразить в общем виде (см. Тичворт и Велч, 1961):

ф(/)=7г2

2„ Т

1=1-

к к

/=1

где S,{f) - преобразование Фурье для сигнала 5,(/).

s{t)=S,{t)-YuPkhit)

P,j{f) - преобразование Фурье дискретной во времени последовательности p,j{n),

определенное выражением

(4.4.57)

Ф) = 1.рМ)"" (4-4.58)

к - номер состояния модулятора. Слагаемое p,j{n) определяет вероятность того, что сигнал Sj{t) передаётся в «-м сигнальном интервале после передачи сигнала Д). Таким образом, {рц{п)} являются вероятностями переходов в матрице вероятностей переходов Р". Заметим, что ,(1) = pj.

Если метод модуляции без памяти, то переданный в каждом сигнальном интервале сигнал не зависит от сигналов, переданных в предьщущих сигнальных интервалах. Спектральная плотность мощности результирующего сигнала в этом случае можно всё ещё выразить в виде (4.4.57), если матрицу переходных вероятностей заменить на

Р\ Рг Рк

Р\ Рг Рк

(4.4.59)

,Pi Рг ••• Рк.

и навязать условие Р" = Р для всех «> 1. Только при этих условиях выражение для спектральной плотности мощности оказывается функцией стационарных вероятностей

состояний {Pi} и, следовательно, ведёт к простейшей форме

2 / .л л к

/=1

«7

(4.4.60)

Видно, что наш предыдущий результат для спектральной плотности мощности линейной модуляции без памяти, определяемый (4.4.18), можно рассматривать как частный случай (4.4.60), в котором все сигналы идентичны, за исключением ряда скалярных множителей, которые передают цифровую информацию (задача 4.30).

Мы также видим, что первое слагаемое в выражении для спектральной плотности мощности (4.4.57) или (4.4.60) состоит из дискретных частотных компонент. Этот линейчатый спектр исчезает, когда

= 0.

(4.4.61)

Условие (4.4.61) обычно навязывается для практических систем связи и легко удовлетворяется подходящим выбором форм сигнала (задача 4.31).

Теперь определим спектральную плотность мощности базовых модулирующих сигналов, описанных в разд. 4.3.2. Сначала рассмотрим NRZ-сигнал, который характеризуется двумя сигналами sXt) = g{t) и sjt) =-g{t), tj\q g(r) - прямоугольный импульс амплитуды А. Для К = 2 (4.4.60) даёт

J j,J

Gift,

G(ff={ATy

sinTi fT

. nfT J

(4.4.62)

(4.4.63)