и в - произвольное событие с отличной от нуля вероятностью, тогда

НОИ от нуля вероятностьк р(а,\в)= \/\=- (21.14)

Мы используем эту формулу в гл. 5 для нахождения структуры оптимального приёмника для системы цифровой связи, в которой события Л,, /=1, 2,. ., , представляют в нашем случае возможные передаваемые сообщения на данном временном интервале, а Р{А) представляют их априорные вероятности, 5-принятый сигнал, подверженный действию шума, который содержит передаваемое сообщение (одно, из А.), а р(А,\в)

является апостериорной вероятностью А, при условии, что наблюдается принятый

сигнал в.

Статистическая независимость. Статистическая независимость двух или большего числа событий - другое важное понятие теории вероятности. Она обычно возникает, когда мы рассматриваем два или больше экспериментов или результатов повторений одного эксперимента Чтобы пояснить это понятие, мы рассматриваем события А и в и их условную вероятность р{А в), которая является вероятностью события А при условии, что

событие в произошло. Предположим, что появление события А не зависит от появления события в. Это значит, что

р{а\в)=Р{а). (2.1.15)

Подставив (2.1.15) в (2.1 13), получаем результат

Р{А,В)-Р{а)р{в). (2.1.16)

Это означает, что совместная вероятность событий А и. В определяется произведением элементарных или собственных вероятностей событий р(А) и р(В). Когда события А и В удовлетворяют соотношению (2.1.16), их называют статистически независимыми.

Например, рассмотрим два последовательных эксперимента бросания кости. Пусть А представляет выборочные точки с чётными номерами {2,4,6} в первом бросании, а В представляет четно нумерованную выборку {2,4,6} во втором бросании. В случае правильной кости мы считаем что вероятность р{А) 3/6=1/2 и /(5)=3/6=1/2. Теперь вероятность совместного исхода - четно нумерованный результат при первом бросании и четно нумерованный результат при втором бросании - является вероятностью результата для девяти возможных пар (ij), i 2,4,6, j 2,4,6, которая равна 9/36 = 1/4. Но мы имеем также

Р{А,В)Р{а)р{в) = \/4.

Таким образом, результаты А \\ В статистически независимы. Точно так же мы можем говорить, что исходы двух экспериментов статистически независимы.

Понятие статистической независимости может быть расширено на три и большее 4ИСЛ0 событий. Три статистически независимых события А\, Aj и Аз должны удовлетворять следующим условиям:

p{a,.a,)p{a,)pM, р{Ал)=р{Л)рМ,

р{а,,а,)=р{аМаЛ р{АЛ,а,)=р{а,)р{а,)рМ-

в общем случае события А;, i=l, 2,..., , являются статистически независимыми при условии, что вероятности совместного наступления 2, 3,... и событий в любой комбинации определяются произведением вероятностей индивидуальных событий.

2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей

Для данного эксперимента, имеющего выборочное пространство S с элементами SeS, мы определяем функцию X(s). область определения которой S, а областью значений является набор чисел на вещественной оси. Функцию X(s) называют случайной величиной. Например, если мы бросаем монету, воз\южными результатами являются орёл (Н) и решка (Т), так что пространство S содержит 2 точки, маркированные как Н и Т. Предположим, что мы определяем функцию X(s) так, что

Таким образом, мы отображаем два возможных результата бросания монеты в виде двух точек (+1) на вещественной оси. Другой эксперимент - бросание игральной кости с возможными исходами S={1, 2, 3, 4, 5, 6}. Случайная переменная, определённая на этом выборочном пространстве, может быть X(s)=s. В этом случае результаты эксперимента отображаются целыми числами {1,. 2, j, 4, 5, 6}. Можно поло)<сить X(s .s, тогда возможные результаты отображаются целыми числами {1, 4, 9, 16, 25, 36}. Это примеры дискретных счучапных величин.

Хотя мы использовали в качестве примеров эксперименты, которые имеют конечное множество возможных исходов, имеется много физических систем, эксперименты в которых дают непрерывные выходные результаты. Например, шумовое напряжение, создаваемое электронным усилителем, имеет непрерьшную амплитуду. Как следствие, выборочное пространство S амплитуд напряжения U G 5 непрерывно и таким же является отображение .V(u)-u. В таком случае случайную величину X называют непрерывной аучайиой ветчиной. Для случайной величины X рассмотрим событие {X <х), где х-

любое вещественное число в интервале (-oo;-i-qo). Определим вероятность этого события как Р{Х < х) II обозначим её как F{x), т.е.

F{x) = P{X<x) ( oa<.v<oo). (2.1.19)

Функция F{x) названа (pyiiKijueu распределения вероятности случайной величины X. Её также называют iiumeepaibHofi {кумулятивной) ф}нк71ией распределения (ИФР). Так как У(\-) это вероятность, то её значения ограничены интервалом 0<F{x)< \. Фактически F{-oo) = 0 и F{<x)) = 1. Например, дискретная случайная величина, полученная при бросании монеты и определённая (2.1.18), имеет ИФР. показанную на рис. 2.1.](аг). Здесь имеются два скачка F(x): один при Л = -1 и другой при Л" = 1. Точно так же случаГшая величина А(л)=л\ полученная при бросании игральной кости, имеет ИФР, показанную на рис. 2.1.1 (/;) В этом случае F(x) имеет шесть скачков, в каждом из х =1,..., 6

Случ J йн\то величину A(.v) обычно обозначают просто Л.

30 " "

F(x)

5/6 4/6 3/6 2/6 1/6

Рис. 2.1.1 Примеры интегральных ф\ нкций распределения двух дискретных с.тучайны-х величин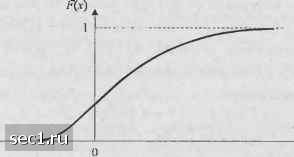

Рис. 2.1.2 Пример интегральной функции распределения непрерывной случайной переменной

ИФР непрерывной случайной величины обычно изменяется так, как показано на рис. 2.1.2. Это гладкая, неубывающая функция. В некоторых практических задачах мы можем также сталкиваться со случайной величиной смешанного типа. ИФР такой случайной величины является гладкой неубывающей функцией в отдельных частях вещественной оси и содержащей скачки в ряде дискретных значений х. Пример такой ИФР иллюстрируется рис. 2.1.3.

Производная от ИФР F(x), обозначаемая как р(х), называется функцией плотности вероятности (ФПВ) случайной величины X. Таким образом, имеем

dFix)

00 < .Y < 00

или, что эквивалентно.

F{x)r p{,,)dH

(- 00 < .тс < ос).

(2.1.20)

(21.21)

Так как F(x) - неубывающая функция, то р(х) > О. Когда случайная величина

дискретная или смешанного типа, ФПВ содержит 5-импульсы в точках нарушения непрерывности F(x). В таких случаях дискретная частьр(х) может быть выражена как

p{xhZP{X = xXx х), (2.1.22)

где X, /"=1, 2,..., п являются возможными дискретными значениями случайной величины; Р(А = г), / -1,2,...», являются вероятностями, а 5(л:)обозначает 5-функцию.