Мы проиллюстрируем этот алгоритм применительно к детектированию сигнала AM с М возможными уровнями. Предположим, что необходимо детектировать информационный символ, переданный на к-и сигнальном интервале,-и пусть г,,,,..../--наблюдаемая принятая последовательность, а D параметр задержки, который выбирается так, чтобы превысить память сигнала, т.е. D> L, где L - присущая сигналу память. На основе принятой последовательности вычисляем апостериорные вероятности

для М возможных позиций символов и выбираем символ с наибольщей вероятностью. Так как

Л = 4„K./..n.ij-..-.) =-7-\-. (5.1.66)

а знаменатель общий для всех символов, правило максимума апостериорной вероятности (МАВ) эквивалентно выбору s\ который максимизирует числитель (5.1.66). Таким образом, правило выбора символа 5* можно записать так:

=arg{maxp(r,,„,r,,.„...r,5<*> = A„)p[s = Д,,)}. (5.1.67)

Если символы равновероятны, вероятности p(j* - можно исключить из вычислений.

Алгоритм для вычисления вероятностей в (5.1.67) рекуррентно начинается с первого символа 5. Имеем

=arg{maxp(r,„...,r..( = А„)р( = А„,)] = = argmaxX...Xp{r,.o,---,-,k""\---)/("-..,Ol- (5.1.68)

= argjmaxI...Zp.("\...,/),

где 5 означает решение об 5, и для математического удобства мы обозначили

р,(5-\...,.>,.<->) = ;7(г,„...,г,.-->,....<-))р(/->,...,.(>). (5.1.69)

Совместную вероятность p{/\...,s~\s] можно опустить, если все символы

равновероятны и статистически независимы. Как следствие статистической независимости последовательности отсчётов аддитивного шума, имеем

р(г,„...,г,к-\....>) =

где мы предположили, что 5* = О для к<0. Для детектирования символа s имеем

(5.1.70)

j-> =. arg

xp(r,,„...,.,. = 4„)p(V = 4,j} =

= argm,x:...5,,,...,r,.<-),....v(>)p(.->....,.)). Совместные условные плотности вероятности в суммах можно выразить так:

(5.1.71)

р{г,,,,...,ф--.. (5.1.72)

Далее совместную плотность вероятности

можно получить через плотности вероятности, вычисленные ранее при детектировании л. Это даёт

Комбинируя (5.1.73) и (5.1.72), а затем подставив их в (5.1.71), получим

=argmax ...j:p.{s-\...JM , (5.1.74)

где по определению

pXs--\...Js-) = p[r2-\.. (5.1.75)

В общем рекуррентный алгоритм для детектирования символа после приёма л* ; -1 • • гi можно записать в виде

S* = arg{maxp(r,,„,r,,,,,...r,5-)?(.)} = = argLxE---ZA(*...,-H

(5.1.76)

I л" .U.U) .U)

1де по определению

p,{s-\...Js) =

1аким образом, рекуррентный характер алгоритма выражается соотношениями (5.1.76,1 и (5.1.77).

Основная проблема с этим алгоритмом - вычислительная сложность. В частности, усреднение, выполняемое над символами в (5.1.76)? требует большое

число вычислений на одном такте принимаемого сигнала, особенно если число М уровней а\шлитуд /4,„} велико. С другой стороны, если М мало и память относительно невелика, эют алгоритм легко выполняется.

5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ

В этом разделе мы определим вероятность ошибки для модулированных сигналов без памяти, описанных в разд. 4.3.1. Сначала рассмотрим сигналы двоичной ЛМ, а затем М -позиционные сигналы различных видов.

5.2.1. Вероятность ошибки при двоичной модуляции

Рассмотрим сигнал двоичной AM, где два сигнала - л-,(/) = g{t) и s-,{t) = -g{t), а g{t) -произвольный импульс, который отличен от нуля на интервале 0<t<T и равен нулю в остальной области.

Поскольку Sjiij-sit), эти сигналы называют противоположньши. Пусть энергия импульса g{t) равна <Г . Как указано в разд. 4.3.1, сигналы AM является одномерными, и, следовательно, их геометрическое представление определяется одномерными векторами •rV -2" ~ л/ - Рисунок 5.2.1 иллюстрирует две сигнальные точки.

Предположим, что два сигнала равновероятны и что передан сигнал s{t). Тогда выходной сигнал (на выходе корреляционной схемы или согласованного фильтра) демодулятора равен

r = s+n = ,+n, (5.2.1).

Рис. 5.2.1. Сигнальные точки для двоичных противоположных сигналов

где п представляет компоненту аддитивного гауссовского шума, которая имеет нулевое среднее и дисперсию а =jNq. В этом случае правило решения, основанное на корреляционной метрике (5.1.44), сравнивает г с нулевым порогом. Если г > О, то решение принимается в пользу Sf{t), а если г <0 - в пользу (O- Ясно, что условные ФПВ для г равны

,-(-А)7>/о

(5.2.2) (5.2.3)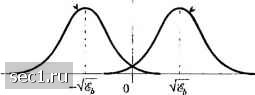

Рис. 5.2.2. Условные ФПВ для двух сигналов

Эти две условные ФПВ показаны на рис. 5.2.2. При условии, что передан сигнал 5,(/), вероятность ошибки определяется вероятностью того, что г <0, т.е.

P{e\s)- ip{r\s,)dr = -j£ехр - L

(5.2.4)

где Q{x) - g-функция, определённая (2.1.97). Аналогично, если предположим, что бьш передан сигнал Sjit), то г = -.j + п и вероятность того, что г>0, также равна

р[е\5,) = (VA/-0) • Поскольку сигналы s{t) и SjU) равновероятны, то средняя вероятность ошибки

(5.2.5)

Мы хотим отметить два важных свойства этой характеристики качества. Во-первых, заметим, что вероятность ошибки зависит только от отношения Щ/Nq и не зависит от