других более детальных характеристик сигналов и шума. Во-вторых, заметим, что 2(f/Ng также выходное отношение сигнал/шум (ОСШо) согласованного фильтра (и коррелятора) демодулятора. Отношение (*5,/Ао обычно называют отношением сигнал/шум на бит.

Отметим также, что вероятность ошибки можно выразить через расстояние между сигналами 5, и s. Из рис. 5.2.1 видно, что два сигнала находятся на расстоянии

= 2д/. Подставив i?; = jdfj в (5.2.5), получим

(5.2.6)

Это выражение иллюстрирует зависимость вероятности ошибки от расстояния между двумя сигнальными точками.

Далее определим вероятность ошибки для двоичных ортогональных сигналов. Повторим, что в этом случае сигнальные векторы s, и являются двухмерными, как показано на рис. 5.2.3, и их можно выразить согласно (4.3.30) так:

St =

(5.2.7)

где /1, обозначает энергию для каждого из сигналов. Заметим, что расстояние между сигнальными точками теперь d - /2 .

Для расчёта вероятности ошибки предположим, что передаётся сигнал s,. Тогда принимаемый вектор на выходе демодулятора

(5.2.8)

Рис. 5.2.3. Сигнальные точки для двоичных ортогональных сигналов

Мы можем теперь подставить г в корреляционные метрики, определяемые (5.1.44),

чтобы получить C(r,s,) и c(r,S2) Вероятность

ошибки - это вероятность того, что

c(r,S2)> c(r,S). Таким образом.

(5.2.9)

P(es,)=p[c(r,s2)>c(r,s,) Поскольку /7 и Ит - статистически независимые гауссовские случайные величины с нулевым средним и дисперсией jNq, то х = ги-пу - гауссовская случайная величина с нулевым средним и дисперсией . Следовательно,

4«2 -"i > = "г- е--" dx = -7= Г е- dx = Q

(5.2.10)

Вследствие симметрии та же вероятность ошибки получается в предположении, что передаётся s,. Следовательно, средняя вероятность ошибки для двоичных ортогональных сигналов

Pb = Q

где по определению у/, - это ОСШ на бит. 218

(5.2.11)

Если сравним вероятность ошибки для двоичных противоположных сигналов с вероятностью ошибки для двоичных ортогональных сигналов, то находим, что ортогональные сигналы требуют удвоения энергии сигнала для достижения той же вероятности ошибки, что в системе с противоположными сигналами. Поскольку 101g2 = 3 дБ, то видим, что ортогональные сигналы на 3 дБ хуже, чем противоположные сигналы. Разница в 3 дБ объясняется тем, что расстояние между двумя сигнальными точками ортогональной системы равно df = 2<+, в то время как расстояние между точками противоположных сигналов равно dfj = 4<*j.

Зависимость вероятности ошибки от 101g<f/7\o для этих двух типов сигналов показана на рис. 5.2.4. Как видно из рисунка, для любой заданной вероятности ошибки требуемое значение <f, / Nq для ортогональных сигналов больше, чем для противоположных сигналов.

10 I

10 2

10-3

10-"

10-5

I0-*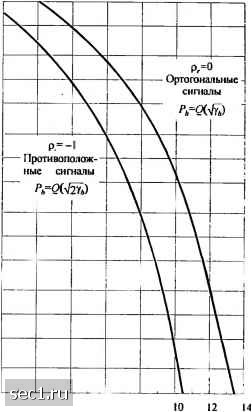

4 6 8 ОСШ на бит. у4,дБ

Рис. 5.2.4. Вероятность ошибки для двоичных сигналов

5.2.2. Вероятность ошибки для М-позиционных ортогональных сигналов

Для ортогональных сигналов равной энергии оптимальный детектор выберет сигнал, который приводит к наибольшей корреляции между принимаемым вектором г и каждым из М возможных к передаче сигнальных векторов {s,„} , т.е.

r-s,„ . =1. 2,М. (5.2.12)

Чтобы рассчитать вероятность ошибки, предположим, что передаётся сигнал s,. Тогда принимаемый сигнальный вектор

r = [ф:+n п, «3 (5.2.13)

где и,, «3, .../7д, - взаимно независимые случайные гауссовские величины с нулевыми средними и дисперсией csI=\Nq.B этом случае выходы набора М корреляторов равны

. (5.2.14)

Заметим, что скалярный множитель <f; можно исключить путём деления всех выходов на д/. Тогда с учётом нормирования ФПВ сигнала на выходе первого коррелятора ( =V + «i) равна

(5.2.15)

a ФПВ сигналов на выходах остальных М -1 корреляторов равны

т = 2,3,М.

(5.2.16)

Математически удобно сначала найти вероятность того, что детектор осуществляет правильный приём. Это вероятность того, что г, больше, чем каждый из М-1 выходов корреляторов «2,Лз,...,и,„. Вероятность этого события определяется так:

- = £ ("2 < г,,Нз < г,,...,< г, г, )р[г, )dr,. (5.2.17)

где р{пт <г,п <t\,...,ni <ii) - совместная вероятность того, что щ,п,...,п меньше, чем г, при данном r. Затем эта совместная вероятность усредняется по всем r. Так как {/;„} статистически независимы, то совместная вероятность определяется произведением М -1 собственных вероятностей вида

1 гг,4Ш:, 2

«... <-.к.)- LPrK)dx„,=i с- dx. (5.2.18)

Л/-1

Эти вероятности одинаковы для /и = 2,3,М, и, следовательно, совместная вероятность приводит к (5.2.18) в степени М-1. Таким образом, вероятность правильного приёма

L"W2n

а вероятность ошибки (к -битового) символа равна

(5.2.19)

n Л/-1

(5.2.20)

dy. (5.2.21)

Такое же выражение для вероятности ошибки получим при передаче любого из других М-1 сигналов. Поскольку все сигналы равновероятны, то выражение по формуле (5.2.21) определяет и среднюю вероятность ошибки. Расчёт по этой формуле можно выполнить численно.

Для сравнения качества различных методов цифровой модуляции желательно иметь зависимость вероятности ошибки от ОСШ на бит <,,/ Ng, вместо ОСШ на символ <f; / Лц.

При М = 2*" каждый символ передаёт к бит информации, и, следовательно, (f, = кё,,. Таким

образом, (5.2.21) можно выразить через / Ло подстановкой .

Иногда также желательно выразить вероятность ошибки символа через эквивалентную вероятность ошибки на бит.

Более общее понятие «эквивалентной вероятности ошибки», которое позволяет сравнивать между собой самые различные цифровые системы (с различными кодами и методами модуляции) в произвольных каналах введено Л.М. Финком [ ] (прп).