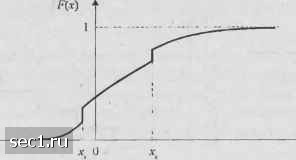Рис. 2.1.3 Пример интегральной функции

распределения случайной переменной смеш;шного типа

Часто мы сталкиваемся с проблемой определения вероятности того, что случайная величина X находится в интервале (зсх), где у>х . Чтобы определить вероятность этого события, начнём с события {А<л%} Это событие всегда можно выразить как объединение двух несовместных событий {A<.y,) и {х<Х<Хт). Следовательно, вероятность события {Х<.т} можно выразить как сумму вероятностей несовместных событий. Таким образом, мы имеем

Р{Х < х) = Р{Х<X,)+Р(х, <Х<х),

F{x,) = F{x,)+P{x<X<x,) или эквивалентное соотношение

Р{х,<Х<х,) = Р{х,) F(x,) = [p{x)dx (2 1.23)

Другими словами, вероятность события {х<Х<х}~это площадь под ФПВ в пределах х<Х<х.

Многомерные случайные величины, совместные распределения вероятностей и совместные плотности вероятностей. Когда имеем дело с комбинированными экспериментами или повторениями одного эксперимента, мы сталкиваемся с многомерными случайными величинами и их ИФР и ФПВ Многомерные случайные величины - в основном многомерные функции - определены на выборочном пространстве при комбинированном эксперименте. Начнём с двух случайных величин Хп Х, каждая из которых может быть непрерывной, дискретной или смешанной. Совместная рштегральная функция распределения (СИФР) для двух случайных величин определяется так:

f{x, , V,)- Р{Х, < г, ,X,<xJ=lJl р{„, )di,, d„, , (2.1.24)

где p(.Y,,.YJ - совместная функция плотности вероятности (СФПВ). Последнюю можно также выразить в виде

p[.hz-F[x„x,). (2.1.25)

Когда СФПВ р{х,х) интегрируется по одной из переменных, мы получаем ФПВ по другой переменной, те.

р{х„ х)dx = р). Гр{х,. x, )dx =р{х}

(2.1.26)

ФПВ р{х) и р(х), полученные путём интегрирования СФПВ по одной из

переменных, называют собственными (маргинальными) ФПВ. Далее, если pi,x,xj интегрировать по двум переменным, получим

1 £, ( 2 = F(oo,oo) = I. (2.1.27)

Заметим также, что F{- со,- qo) = f{- qo,x, ) = F{x,- оо) = О.

Обобндение вышеуказанных соотношений на многомерные случайные величины очевидно. Предположим, нгоХ,, /=1, 2,..., н, являются случайными величинами с СИФР F(x„x„ .,x„)=P{X,<x„X,<x,,..,X„<xJ =

= I -1 p{u,n.,.,u„)du,du..du„,

« -00 J-CO J

где p(x,,.Y,, ..,х„) - совместная ФПВ. Беря частные производные от F(x,,X3, .,х„), заданной (2.1.28), получаем

р{х„х„...,х„)= f F(.x„x, , ..,xj. (2.1.29)

Любое число переменных в /7(х,,х,,...,х„) можно исключить путём интегрирования по этим переменным Например, интегрируя по Хг и Хз, получаем

Г p{xuX ,x,,...,x„)dxdx =/7(х„Х4,..,х„). (2.1.30)

J- со J-00

Следуеттакже, что f(x„oo,oq,x4,. ,х„)= f(x,,.X4,X5, ..,х„), а f(x,,-c»,-oo, X4,..,xj=0.

Условные функции распределения вероятности. Рассмотрим две случайные величины и 2 с СФПВ р(.х,,х,). Предположим, что мы желаем определить вероятность того, что случайная величина Х\ < xi при условии, что

.Хз-ДХз <Х <х,

где Ах,- некоторое положительное приращение. Таким образом, мы желаем определить вероятность события < х, х,-Ах, < А, < х,). Используя соотношения, приведённые ранее для условной вероятности события, вероятность события (л, <х,х,-Ах, <X,<x можно определить как вероятность совместного события (Х, <х,,х,-AXj <<х,), делённую на вероятность события (Х - АХ < < ATj). Таким образом.

Р(Х < X, х, - Axj < < =

ч

(2 1.31)

(Х, X,)- F(x,, - Ах,) F(x,)-F(,-Ax,)

Предполагая, что ФПВ р(Ху,х) и pix) являются непрерывными функциями на интервале (х,-Ах,, х), мы можем делить числитель и знаменатель (2.1.31) на и взять предел при AXj -> О . Таким образом, мы получим

L Л1 J-со

(2.1.32)

3-56

что является условной ИФР случайной величины Xi при заданной величине Xj. Заметим, что F(-ooXt) = 0 и F(cox) = l. Путём дифференцирования правой части (2.1.32) по xi мы

получаем условную ФПВ ;;(х, х,) в форме

(2.1.33)

В качестве альтернативы мы можем выразить совместную ФПВ р{х,х.,) через

условную ФПВ /?(х,х2) или р(х\х) как

Р х,)Р {х\х, )р (х,) = р (х,х, )р (х,). (2.1.34)

Обобщение соотношений, данных выше, на многомерные случайные величины не вызывает затруднений. Начиная с совместной ФПВ случайных величин X,, /=1, 2,...,/у, можно написать

/7(x„.X2,...,x„)=p(x„X2,...,xJx„...,x„)p(x,,...,x„), (2.1.35) где к - любое целое число в пределах \<к <п. Совместная условная ИФР, соответствующая СФПВ р{х, х,..., xj. х,,,..., х„), равна

p{it,u.,,...,iix,...x)dii dii., ...diL

./(х,,Х2,...,Х *+1»->я)~

(2.1.36)

Условные ИФР удовлетворяют соотношениям, ранее установленным для таких функций, таким как

/(oo,X2,...,Xj х,,...,х,)=/(х2,Хз,...,х. Х,...,Х„ F(-oo,x2,...,x,x,,„...,xJ=0.

Статистически независимые случайные величины. Мы уже определили статистическую независимость двух или больше событий из выборочного пространства S. Понятие статистической независимости может быть распространено на случайные величины, определённые на выборочном пространстве и полученные при комбинированном эксперименте или при повторении единственного эксперимента. Если эксперименты приводят к несовместным исходам, вероятность результата в одном эксперименте не зависит от результата в любом другом эксперименте. Т.е. совместная вероятность результатов определяется произведением вероятностей, соответствующих каждому результату. Следовательно, случайные величины, соответствующие результатам в экспериментах, независимы в том смысле, что их СФПВ (или СИФР) определяется произведением соответствующих ФПВ (или ИФР). Следовательно, многомерные случайные величины статистически независимы, если, и только если

/(x„X2,...,x„)=F(x,HxJ-F(xJ, (2.1.37)

или в качестве альтернативы

р(х„Х2,...,х„)= ;?(х,)р(х,) р{х„). (2.1.38)

Правильнее было бы говорить о зависимых и независимых событиях безотносительно к способу проведения эксперимента (прп)