10-»

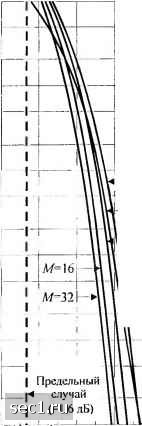----М=4 (ФМ)

-4 0 4 8 12 16 . ОСШ па бит, у,„дБ

Рис. 5.2.6. Вероятность ошибки на символ для биортогональны.х сигналов

101g{l-p) = 101g дБ. (5.2.35)

Для М = 2 экономия составит 3 дБ. Однако по мере увеличения М экономия в ОСШ стремится к О дБ.

5.2.5. Вероятность ошибки для М-позиционной системы с двоичными кодовыми сигналами

Мы видели в разд. 4.3, что двоичные кодированные сигналы можно представить сигнальным вектором

\,=к , „.л "2 = 1, 2,..., М, где .v„ = ±.Jd7N для всех т и j , j\ - длина

кодового блока, и она является также размерностью М-позиционного сигнала.

Если dl - минимальное евклидово расстояние между парой сигналов из М возможных, тогда вероятность ошибки приёма кодового блока определяется верхней границей так:

;„<(м-1)р,=(м ])Q

<2* ехр

\.*lПlll /

47V„

(5.2.36)

Величина минимального евклидова расстояния будет зависеть от выбора кодовых слов, синтеза кода.

5.2.6. Вероятность ошибки для М-позиционной AM

Напомним, что М-позиционные сигналы AM представляются геометрически как М одномерных сигнальных точек со значениями

«,=л/НД., « = 12,...,М. (5.2.37)

где (f..- энергия базового сигнального импульса g{l). Значения амплитуд можно выразить

гак:

Д„=(2ш-1-М), т = \,2,-.,М, (5.2.38)

где евклидово расстояние между соседними сигнальными точками равно dJl.

Средняя энергия сигнала

Л d-ir. . .., d\

cp=-E,„-;(2--l-M)=[iM(M-l)]4(M l)d\. (5.2.39)

Эквивалентно мы можем характеризовать эти сигналы их средней мощностью, которая равна

ср=- = Км-1). (5.2.40)

Средняя вероятность ошибки для М-позиционной AM можно определить из правила выбора решения по максимуму метрик корреляции, определяемых (5.1.44). Эквивалентно детектор сравнивает выход демодулятора г с рядом М-\ порогов, которые располагаются в средних точках между соседними уровнями амплитуд, как показано на рис. 5.2.7.

Рис. 5.2.7. Расположение порогов в средних точках между соседними уровнями амплитуд

Таким образом, решение выбирается в пользу уровня амплитуды, который расположен ближе всех к г.

Расположение порогов, указанных на рис. 5.2.7, помогает в вычислении вероятности ошибки. Заметим, что если передаётся /п-й амплитудный уровень, то выход демодулятора равен

r = s,+n = A„,+n, (5.2.41)

где компонента шума п имеет нулевое среднее и дисперсию а] =jNq. В предположении, что все уровни амплитуд априори равновероятны, средняя вероятность ошибочного приёма символа равна вероятности того, что компонента шума п превосходит по амплитуде половину расстояния между соседними уровнями. Однако, когда передаётся один из двух крайних уровней ±(М-1), ошибка возникает только в одном направлении. Таким образом, мы имеем

/ -

Mzii 2 г „-v72 . 2(М-1) J

(5.2.42)

Вероятность ошибки (5.2.42) можно также выразить через среднюю переданную мощность. Из (5.2.40) видно, что

PJT.

(5.2.43)

Подставив "<f, в (5.2.42), получим среднюю вероятность ошибки на символ для AM через среднюю мощность:

или, что эквивалентно.

2(М-1) бг

(5.2.44)

(5.2.45)

где (fp = РрГ средняя энергия. При построении зависимости вероятности ошибки на

символ М-позиционной системы AM обычно используется ОСШ на бит как базовый параметр. Так как Т=кТ и к = logj М, (5.2.45) можно преобразовать к

2(М-1) М

(61og2 М),

(5.2.46)

гае ifp = Рср - средняя энергия на бит, а dbp/N - средняя ОСШ на бит.

10-1

10-2

2 о о

IO-J

= 10 -

I0-*

Рисунок 5.2.8 иллюстрирует зависимость вероятности ошибки на символ от

lOlg ifjp/Ao) со значением М в качестве параметра.

Заметим, что случай М = 2 соответствует вероятности ошибки для двоичной системы противоположных сигналов. Также видим, что при фиксированной вероятности ошибки Рм ОСШ на бит возрастает более чем на 4 дБ при каждом удвоении числа М. При очень больших М требуемый рост ОСШ при удвоении числа М приближается к 6 дБ.

-6 -4 -2 о 2 4 6 8 10 12 14 16 18 20 22 ОСШ на бит, Уд.дБ

Рис. 5.2.8. Вероятность ошибки на символ дпя AM

5.2.7. Вероятность ошибки для М-позиционной ФМ

Напомним из разд. 4.3, что цифровой сигнал ФМ можно выразить так:

s„.U) = git)COS 2nfj+{m-l) и он имеет векторное представление

1<7п<М, 0<t<T,

Дсов{т-\) 7sin(w-l)

(5.2.47)

(5.2.48)

где if, =i.-энергия каждого сигнала, а g(/) - огибающая импульса передаваемого

сигнала. Поскольку сигналы имеют одинаковую энергию, оптимальный детектор в канале с АБГШ, определяемый (5.1.44), вычисляет корреляционные метрики