C(r,sj = r-s„„ /и = 1,2,..., М.

(5.2.49)

Другими словами, принимаемый сигнальный вектор г = [г1 г2 проектируется на М

возможных сигнальных векторов, и решение принимается в пользу сигнала с наибольшей проекцией.

Корреляционный детектор, описанный выше, эквивалентен фазовому детектору, который определяет фазу принимаемого сигнала г и выбирает сигнальный вектор s„,, фаза которого ближе всего к фазе г. Поскольку фаза г равна

0 =arctg-,

(5.2.50)

мы хотим определить ФПВ 0, по которой сможем вычислить вероятность ошибки.

Рассмотрим случай, когда фаза передаваемого сигнала 5,(/) равна 0=0. Следовательно, вектор переданного сигнала

(5.2.51)

а вектор принимаемого сигнала имеет компоненты

(5.2.52)

Поскольку и, и «2 являются совместно гауссовскими случайными величинами с нулевыми средними, следует, что r и являются совместно гауссовскими случайными

величинами с e{r) = , е{гт) = О и = а]. =\Nq = cs]. . Следовательно,

2 ехр

(5.2.53)

ФПФ фазы 0,. можно получить заменой переменных (/"1,) на

0, = arctg(r2/r,). Это даёт совместную ФПВ

(5.2.54)

F4,-27Fcos0/ 21

Р;.0,(.0.) = ехр -

Интегрирование р {y,Qf) по области V даёт

Ре,[®) - P.y®iV = е--"« Ve---:fldV . (5.2.55) где для удобства мы обозначили ОСШ символом =JNq . Рисунок 5.2.9 иллюстрирует Рд (о) для различных значений параметра ОСШ у, когда фаза переданного сигнала

равна нулю Заметим, что РеДОг) становится уже и более концентрированной около фазы 0 = О по мере увеличения параметра ОСШ у,.

Когда передаётся 5(/), ошибочное решение произойдёт, если шум вызовет нахождение фазы у J вне области -n/M<Q<n/M.

Автор на протяжении всей книги обозначает случайные величины (процессы) то прописными (как обычно принято), то строчными буквами. Ввиду большого объёма материала мы не стали вносить соответствующих изменений (прп).

1.61

1,43 1,25 I-

Y.= 10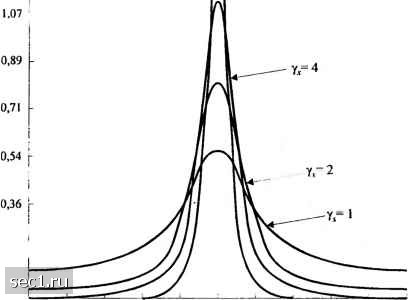

0,18 г

-3,14 -2,51 -1,88 -1,26 -0,63 0,00 0,63 1,26 1,88 2,51 3,14

Рис. 5.2.9. Функция плотности вероятности pe,(Q,) для у,= 1,2,4 и 10

Следовательно, вероятность ошибочного приёма символа

=1-Се.КК- (5-2.56)

В общем, интегрирование (©,) не приводится к простой форме и следует

выполнить численное интегрирование, исключая случаи М = 2 и М = 4.

Для двоичной фазовой модуляции два сигнала s{t) и sit) противоположны, и, следовательно, вероятность ошибки

(5.2.57)

Когда М = 4, имеем случай двух двоичных фазово-модулированных сигналов в квадратуре. Поскольку здесь нет переходных помех или интерференции между сигналами на двух квадратурных несущих, вероятность ошибки на бит идентична той, которая определяется (5.2.57). С другой стороны, вероятность ошибки на символ при Л/= 4 определяется с учётом того, что

2 No)

(5.2.58)

где P. - вероятность правильного приёма для двух битовых символов. Результат (5.2.58) следует из статистической независимости шума на квадратурных несущих. Следовательно, вероятность ошибки на символ для М = 4 равна

(5.2.59)

Для М>4вероятность ошибки на символ Р получена численным интегрированием (5.2.55). Рисунок 5.2.10 иллюстрирует эти вероятности ошибки как функции ОСШ на бит для Л/=2, 4, 8, 16 и 32.

се S S

10-2

10-3

Э о л

g 10-4

8. -

10-5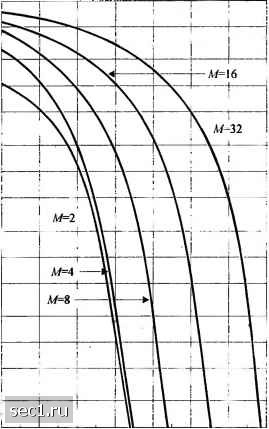

4 8 12 16 ОСШ на бит, у.дБ

20 24

Рис. 5.2.10. Вероятность ошибки на символ для сигналов ФМ

Кривые явно иллюстрируют потери в ОСШ на бит по мере роста М>4. Например, при P =10~* разница в ОСШ между М = 4 и М = 8 приблизительно равна 4 дБ, а разница между М = 8и М = 16 приблизительно равна 5 дБ. Для больших значений М рост числа фаз вдвое требует дополнительного увеличения ОСШ на 6 дБ/бит для достижения того же качества.