Здесь X и у являются некоррелированными гауссовскими случайными величинами с одинаковой дисперсией а] N,. Фаза равна

О, =arctg(>/x). (5.2.68)

На этой стадии мы имеем проблему, которая идентична той, которую мы решали ранее для фазово-когерентной демодуляции. Единственная разница в том, что дисперсия шума теперь в два раза больше, чем в случае ФМ. На этом основании заключаем, что характеристика качества ДФМ на 3 дБ хуже, чем для ФМ. Этот результат относительно хорош для М>4, но он пессимистичен для Л/= 2 в том смысле, что действительная потеря ДФМ относительно ФМ менее 3 дБ при больших ОСШ. Это мы покажем ниже.

В двоичной ДФМ два возможных значения фазы передаваемого сигнала равны О и я. Как следствие, только реальная часть ггД, необходима для извлечения информации. Используя (5.2.67), выразим реальную часть так:

Поскольку мы предполагали, что разность фаз между сигналами на соседних интервалах равна О, ошибка

возникает, если Re(ir )<0.

Вероятность того, что это специальный случай исследования, данного в приложении В, где обсуждается вероятность того, что общая квадратичная форма комплексных случайных гауссовских величин меньше нуля. Общая форма для этой вероятности даётся (В.21) в приложении В, и она зависит всецело от первого и второго моментов комплексных гауссовских

10-=

случайных величин и

г ,. Вычислив

10-3

10-5

10-«

моменты и параметры, которые являются функциями моментов, получим вероятность ошибки двоичной ДФМ в

виде

i-ie""-, (5.2.69)

где Yj, = \INq - это ОСШ на бит.

Графики (Уй) показаны на рис. 5.2.12. На этом графике показана также вероятность ошибки двоичной когерентной ФМ.

Видно, что при вероятности ошибки Р<\(У разница в ОСШ между ФМ и ДФМ менее 3 дБ. При < 10 * разница в ОСШ меньше 1 дБ.

о 2 4 б 8 10 ОСШ на бит. Г4.дБ

Рис. 5.2.12. Вероятность ошибки для двоичной ФМ и ДФМ

Этот результат можно получить значительно проще (см. Л.М. Финк [ ]) из формулы для вероятности ошибки двоишой системы сигналов, ортогональных в усиленном смысле, если учесть, irro сигналы двоичной ДФМ на интервале 27" ортогональны в усиленном смысле (прп).

10-:

ю-"

10-«

4 б 8 10 ОСШ на бит, Yj, дБ

Рис. 5.2.13. Вероятность ошибки на бит ддя двоичной и четырёхфазной ФМ и ДФМ

Вероятность ошибки на бит для четырёхфазной ДФМ с кодом Грея можно выразить через известные функции.

Мы просто сформулируем здесь результат, а читателю, интересующемуся деталями, рекомендуем приложение С. Результат выражается в виде

где Oy{ab) - это О-функция Маркума, определенная (2.1.122) и (2.1.123). /о(х) - модифицированная функция

Бесселя нулевого порядка, определённая (2.1.120), а параметры а и h определяются так:

-27,(1-7172),

6 = 27,(1 + 7172).

Рисунок 5.2.13 зависимость вероятности бит для сигналов двух- и четырёхфазной ДФМ и когерентной ФМ, полученную расчётом по точным формулам этого раздела.

(5.2.71)

иллюстрирует ошибки на

Поскольку двоичная ДФМ мало уступает двоичной ФМ при больших ОСШ и не требует разработки специального метода оценки фазы несущей, она часто используется в цифровых системах. С другой стороны, четырёхфазная ДФМ приблизительно на 2,3 дБ хуже по качеству, чем четырёхфазная ФМ при больших значениях ОСШ. Следовательно, выбор между этими двумя четырёхфазными системами неоднозначен. Надо взвесить потери в 2,3 дБ и упрощения в реализации устройства.

5.2.9. Вероятность ошибки для ICAM

Напомним из раздела 4.3, что сигнал КАМ можно выразить так

Л) - Ag(t)coslTifJ - Agit) smlnfj, (5.2.72)

где A и /4 - содержащие информацию амплитуды квадратурных несущих, а g{t)-сигнальный импульс. Векторное представление этих сигналов

(5.2.73)

g na\2 g

Чтобы определить вероятность ошибки при КАМ, мы должны конкретизировать точки сигнального созвездия. Начнём с сигнального ансамбля КАМ, который имеет М =4 точки. Рис. 5.2.14 иллюстрирует два таких ансамбля. Первый (а)-это четырёхфазный модулированный сигнал, а второй (6) - это четырёхфазный сигнал КАМ с двумя уровнями амплитуд, обозначенными Л, и А, и четырьмя значениями фаз. Поскольку вероятность ошибки определяется минимальным расстоянием между парой сигнальных точек, примем

условие, что dl = 2а для обоих сигнальных созвездий, и рассчитаем среднюю переданную мощность, основываясь на предположении, что все сигнальные точки равновероятны. Для четырёхфазного сигнала имеем

р=\{4)2а=2а\ (5.2.74)

Для двухамплитудной четырёхфазной КАМ мы разместим точки на окружностях радиуса а и а . Поскольку d =2л, имеем

ср =i[2(3) + 2]=2. (5.2.75)

что совпадает со средней мощностью для четырёхфазного сигнального созвездия. Следовательно, для всех практических применений вероятность ошибки двух ансамблей сигналов одинакова. Другими словами, нет преимущества двухамплитудного сигнала КАМ относительно четырёхфазной модуляции.

d=Zi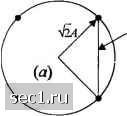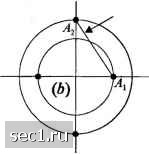

Рис. 5.2.14. Два 4-точечных сигнальных созвездия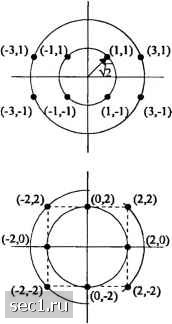

(«)

Рис. 5.2.15. Четыре 8-точечных созвездия сигналов КАМ

Далее рассмотрим восьмиуровневый (Л/= 8) сигнал КАМ. В этом случае имеются много возможных сигнальных созвездий. Рассмотрим четыре сигнальных созвездия, показанных на рис. 5.2.15. Все они характеризуются двумя амплитудами и имеют

минимальные расстояния между сигнальными точками 2а. Координаты [а, А) для