его полоса частот w приближённо равна обратной величине т. Таким образом, w~мт, и поскольку t=k/r = (log, m)/r , то следует

Таким образом, по мере роста М требуемая полоса частот уменьшается при фиксированной битовой скорости r. Частотная эффективность измеряется отношением битовой скорости к полосе и равна

§=og,m. (5.2.84)

Частотно-эффективный метод передачи сигналов AM - это однополосная передача. Тогда полоса, требуемая для передачи сигнала, приблизительно равна 1/2Г, и, поскольку

t=k/r= (log, m)/r , следует, что

f = 21og2M. (5.2.85)

Это в два раза лучше, чем при ФМ.

В случае КАМ имеем две ортогональные несущие, причём на каждой несущей передаётся AM сигнал. Таким способом удваиваем скорость относительно AM. Однако сигнал КАМ должен быть передан двумя полосами. Следовательно, КАМ и AM имеют одинаковую частотную эффективность, если полоса относится к полосовому сигналу.

Ортогональные сигналы имеют в целом другие требования по полосе. Если М = 2* ортогональных сигнала синтезированы посредством ортогональных несущих с минимальным разносом частот 1/2Г для ортогональности, то полоса частот, требуемая для передачи к = log, М информационных бит, равна

ММ м

в этом случае полоса увеличивается по мере увеличения М. Аналогичные соотношения можно получить для симплексных и биортогональных сигналов. В случае биортогональных сигналов требуется полоса частот, равная половине полосы для такого же количества ортогональных сигналов.

Компактное и осмысленное сравнение этих методов модуляции базируется на зависимости нормированной скорости передачи данных r/w (бит в секунду на 1 Гц полосы частот) от ОСШ на бит (%/Nq), требуемого для достижения заданной вероятности ошибки. Рисунок 5.2.17 иллюстрирует зависимость r/w от ОСШ на бит для AM, КАМ, ФМ и ортогональных сигналов для случая, когда вероятность ошибки на символ

= 10 Видим, что в случае AM, КАМ и ФМ рост М ведёт к росту r/w. Однако плата за достижение большей скорости передачи данных увеличивается по мере роста ОСШ на бит. Следовательно, эти методы модуляции предпочтительны для частотно-ограниченных каналов связи, когда желательно иметь r/w>1 и где обеспечивается достаточно высокое ОСШ, чтобы поддержать рост М. Телефонные каналы и цифровые микроволновые радиоканалы являются примерами таких частотно-ограниченных каналов.

В противоположность этому М-позиционные ортогональные сигналы дают отношение битовой скорости к полосе канала rjw <\. При росте М величина r/w падает из-за роста

Такой разнос частот является минимально необходимым для разделения сигналов при когерентном приёме (прп).

требуемой полосы частот канала. Однако ОСШ на бит, требуемое для достижения заданной вероятности ошибки (в нашем случае Рм=10"), уменьшается с ростом М. Следовательно, Л</-позиционные ортогональные сигналы предпочтительны для каналов с ограничением по мощности, которые имеют достаточно широкую полосу для размещения большого числа сигналов. В этом случае, когда М оо, вероятность ошибки можно сделать сколь угодно малой, если обеспечено /Ло> 0,693 (-1,6 дБ). Это минимальные ОСШ на бит, требуемые для достижения реализуемой передачи в пределе, когда -> оо и соответствующее отношение битовой скорости к полосе частот RJW О.

На рис. 5.2.П также дан график нормированной пропускной способности частотно-ограниченного канала с АБГШ, полученный Шенноном (1948). Отношение C/W, где C=R-это пропускная способность в битах/с, представляет наибольшее достижимое отношение битовой скорости к полосе в данном канале. Следовательно, оно служит верхней границей частотной эффективности для любого вида модуляции. Эта граница определяется в гл. 7 и там же детально обсуждается.

5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ

Напомним, из разд. 4.3, что МНФ-это метод модуляции с памятью. Память обусловлена непрерывностью фазы передаваемой несущей от одного сигнального интервала к другому. Передаваемый МНФ сигнал можно записать в виде

s(/) = co{2цfJ + ф)\, (5.3.1)

где ф(/; l) - фаза несущей. Отфильтрованный принимаемый сигнал r{t) и шум n{f) в канале представим так:

г{() = ,{{)+?,{(), (5.3.2)

я(/) = COS271/;/ -/;,(/)sm2nfj . (5.3.3)

5.3.1. Оптимальные демодуляция и детектирование для МНФ

Оптимальный приёмник для этих сигналов состоит из каскадного соединения коррелятора и детектора последовательности максимального правдоподобия, который ищет путь по решётке состояний с минимальным евклидовым расстоянием от принятого сигнала. Алгоритм Витерби позволяет эффективно осуществить этот поиск. Установим общую структуру решётки состояний для МНФ и затем опишем расчёт метрик.

Напомним, что фазу несущей для сигнала МНФ с фиксированным индексом модуляции А можно выразить так:

ф(/;1) = 2яЛ2 у(/-Л7-) =

„ (5.3.4)

nhYh+2nh J]lMt-kT) = e„+Q{(,ll пГ</<{п + ])Т,

где мы предположили, что q{f) = О для / < О, q{t) = для t > LT и

lil) = Jlgic)dx. (5.3.5)

Сигнальный импульс g{t)-0 для /<0и (>LT. Для L = l имеем МНФ с полным откликом, а при L>\, где L - положительное целое число, имеем МНФ с парциальным откликом.

Широкие исследования зависимости между энергетической и частотной эффективностью различны.ч систем связи выполнены А.Г. Зюко [48] (прп).

М=64КАМ Л#8АФМ (ОМ)

Асимптота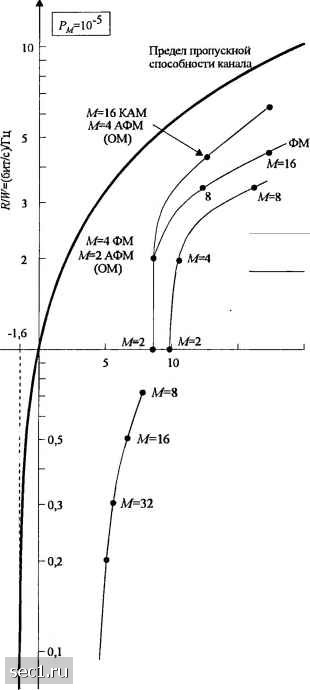

Область малых частотных ресурсов: RJtV> 1

15 20

ОСШ на бит, у.дБ

Область малой энергетики; R/W < 1

М=64

Ортогональные сигналы Когерентное детектирование

Рис. 5.2.17. Сравнение различных методов модулящш при вероятности ошибки на символ 10"

Теперь если h - рациональное число, т.е. h = m/p, где тир - это взаимно простые положительные целые числа, то схему образования МНФ можно представить решёткой. В этом случае имеются р состояний фазы

ят 2im (р - \)жт

если т - четно, и 2р .состояний фазы