2тип {2р-\)пт

(5.3.7)

PP. Р

если т - нечётно. Если Z, = 1, это единственное состояние решётки. С другой стороны, если L>1, имеем дополнительное число состояний, обусловленных парциальным откликом сигнального импульса g{t)., Эти дополнительные состояния можно определить,

выражая 9(/;l) через (5.3.4):

е(/;1) = 2яА I,qit-kT) + 2KhI„git-nT). (5.3.8)

к=п L+1

Первое слагаемое в правой части (5.3.8) зависит от последовательности информационных символов {l„-i,„-2,--,h-L+\) которую называют коррелированным вектором состояний, и представляет слагаемое фазы, которое соответствует сигнальным импульсам, которые ещё не достигли финальных значений. Второе слагаемое в (5.3.8) представляют вклад фазы, обусловленный самым последним символом 1. Таким образом, состояние сигнала МНФ (или модулятора) в точке (-пТ можно выразить как комбинацию фазового состояния и коррелированного состояния, обозначаемую так:

„ = {9«,-,/„-2,-,Ct.,} (5.3.9)

для сигнального импульса с парциальным откликом длины LT, где L>\. В этом случае число состояний равно

(«» чётное).

о (5.3.10)

Арм нечётное).

Теперь предположим, что состояние модулятора в точке / = пТ есть . Влияние нового символа в интервале w7</<(и+1)7" сводится к изменению состояния от S„ до 5„,. Следовательно, в точке t - (и+ l) Г состояние становится

Пример 5.3.1. Рассмотрим схему образования двоичной МНФ с индексом модуляции h = 3/4 и импульсом с парциальным откликом с L-2. Определим состояние схемы МНФ и вычертим фазовое дерево и решётку состояний.

Сначала отмечаем, что имеется 2р = 8 состояний фаз, именно

0, = {о,±71,±1я,±я,я,}.

Для каждого из этих состояний фаз имеется два состояния, которые обусловлены памятью схемы МНФ. Следовательно, общее число состояний М-\в, именно

(0,1) (0,-1) (я,1) (я,-1) (я.1) (я,-1) (я.1) (я,-1) (я.1) (я,-1) (-я,1) (-я.-1) (-я.1) (-я.-1) (->,1) (-я.-1) Если система находится в фазовом состоянии 9 = - 4 я и /„ , = -1, тогда

Решётка состояний иллюстрируется рис. 5.3.1. Путь по решётке состояний, соответствующий последовательности (1,-1,-1,-1,1,1), показан на рис. 5.3.2.

(e„.4-i)

(0.1)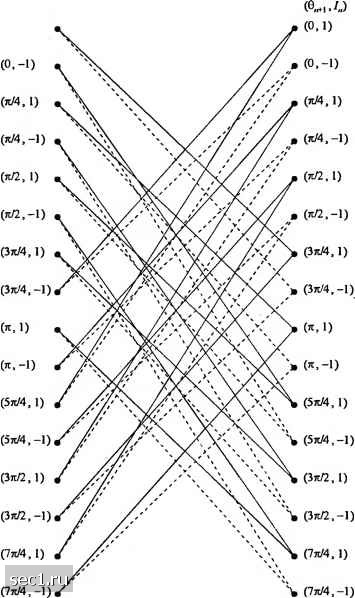

Рис 5.3 1. Решетка состояний для МНФ с парциальным откликом {L=2) с Л=3/4

Для того чтобы нарисовать фазовое дерево, мы должны знать огибающую сигнального импульса g{t). Рисунок 5.3.3 иллюстрирует фазовое дерево, когда g(/) является

прямоугольным импульсом длительности 2Т с начальным состоянием (o,l).

Установив отображение решётки состояний для МНФ, рассмотрим расчёт метрик, формируемых алгоритмом Витерби.

Расчёт метрик. Возвращаясь к математическим основам демодулятора максимального правдоподобия, данным в разд. 5.4.1, легко видеть, что логарифм условной плотности вероятности наблюдаемого сигнала r{t) при условии передачи последовательности символов I пропорционален метрике взаимной корреляции

"(i) = rr-Wc+фО;Ф = +£j"%(/)cos[(o,/+еО; 1)+е„Ц (5.з.11)

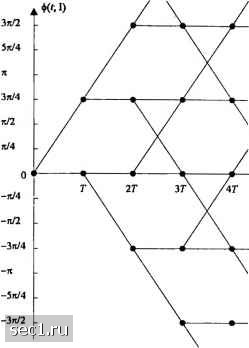Рис. 5.3.3. Фазовое дерево для МНФ с парциальным откликом, (L=2) с /1=3/4

Слагаемое CM„ ,(l) представляет метрики выживших путей (последовательностей) до момента и Г, а слагаемое

"(lQj"tr"W°4+Q(l) + Q"] (5. 12)

представляет дополнительный прирост метрики, вносимый сигналом на интервале времени яГ</<(« + !)Г. Заметим, что имеются возможных последовательностей

I = (/„,/„ ,,...,I„ Li) символов ир (или 2р) возможных состояний фазы {9„}.

Следовательно, имеем рМ (или IpM) различных величин v(l;9„), вычисляемых на каждом сигнальном интервале, и каждая величина используется для прироста метрик, соответствующих рМ~ выживших последовательностей от предыдущего сигнального

интервала. Общая блок-схема на рис. 5.3.4 иллюстрирует вычисления v(l;9„) для декодера Витерби.

Заметим, что число выживших последовательностей в каждом состоянии для процесса декодирования по Витерби равно /?М" (или 2рМ~). Для каждой выжившей

последовательности мы имеем М новых приращений v„(l;9„), которые прибавляются к существующим метрикам, чтобы получить рМ (или 2/?М) последовательностей с рМ (или 2рМ) метриками. Однако их число затем снова уменьшается до рМ (или