2 рМ ) выживших траекторий с соответствующими метриками за счёт выбора наиболее вероятной последовательности из М последовательностей, сливающихся в каждом узле решётки и отбрасывания остальных М -1 последовательностей.

<0

cos 2(iiJ

-sill v)J

cos[9(/;I>H3.]

Фазовый

генератор

9(r,I)4-9

sm[9(r,I>f9]

К декодеру Витерби

Рис. 5.3.4. Вычисление приращений метрик o„(/;9)

5.3.2. Характеристики качества сигналов МНФ

При расчете характеристик качества сигналов МНФ, достигаемого при максимально правдоподобном последовательном оценивании Ml 1110 (MLSE), мы должны определить минимум евклидова расстояния путей по решётке, которые начинаются в некотором узле в момент / = 0 и возвращаются в более позднее время в тот же узел. Как мы теперь покажем, расстояние между двумя путями на решётке относится к соответствующим сигналам.

Предположим, что имеем два сигнала s.{t)n Sj{t), соответствующие двум фазовым

траекториям ф(/; I,) и ф(/; 1). Последовательности I, и 1 должны отличаться в первом

символе. Тогда евклидово расстояние между двумя сигналами на интервале длиной NT, где \/Т - скорость передачи символов, определяется так:

2 (NT \ [ \

= 2Nd-2-] COS а J + \t;\

Т Jo

= 2Nn-2\ со8[ф(/; I,) - ф( I,)

= f Гk-4*0)-Ф( (5-3.13)

Следовательно, согласно (5.3.13) евклидово расстояние сводится к разности фаз между путями на решётке состояний.

Желательно выразить расстояние dfj через битовую энергию. Поскольку 8 = log. Л/,

(5.3.13) можно выразить так:

СО8(0/+ф(/,1 dt =

где 5 определено как

Далее видим, что ф(г; 1,) - ф(/; 1) = ф(/, I, -1), так что, обозначив = I, -1., (5.3.15) можно переписать в виде

5,; = Г{1-ф(-;ф, (5.3.16)

где любой элемент из может принять значения 0,±2,±4,...±2(Л/-1), кроме д, которое не может быть равным 0.

Вероятность ошибки МНФ определяется слагаемым 5,, соответствующим

минимальному евклидову расстоянию, и ее можно выразить так;

= К, О

(5.3.17)

(5.3.18)

Заметим, что для обычной двоичной ФМ без памяти N - \ и = 5 = 2. Следовательно, (5.3.17) согласуется с нашим прежним результатом.

Поскольку 5,„ характеризует качество МНФ с МППО, мы можем исследовать влияние на изменения объёма алфавита М, индекса модуляции h и длительности переданного импульса в системе МНФ с парциальным откликом.

Прежде всего рассмотрим МНФ с полным откликом {L-\). Если возьмем сначала М= 2, то заметим, что последовательности

I, =+1,-1./2>

1=-1+1 / / <5•3l)

которые отличаются при к = 0;\ и совпадают при к>2, приводят к двум фазовым траекториям, которые сливаются после второго символа. Это соответствует разностной последовательности

= {2,-2.0,0,...}: (5.3.20)

Евклидово расстояние для этих последовательностей легко вычислить из (5.3.16), а затем найти верхнюю границу для 5;„. Эта верхняя граница для М -2 равна

з1п2яЛ

am 2

2ith

М = 2.

(5.3.21)

Например, когда h = \, что ведет к ММС, имеем d\{ = 2, так что 5,(i) < 2. Для М > 2 и при полном отклике МНФ также можно легко увидеть, что фазовые траектории сливаются при t = 2T. Следовательно, верхнюю границу 5,„ можно получить,

рассматривая последовательности разностей фаз = {а,-а,О,О,...}, где

а = ±2.±4,...,±2(М-1). Эти последовательности дают верхнюю границу

51п2ккН\]

2knh

Графики зависимости dl{h) от h для М = 2, 4, 8, 16 показаны на рис. 5.3.5.

Из этих графиков очевидно, что большие выигрыши в качестве можно достичь увеличением объема алфавита М Надо вспомнить, однако, что 5„(/г) <c/j(/i). Это значит, что верхняя граница не достижима для всех значений h.

Минимальное евклидово расстояние 5 (/») было определено расчетом по (5.3.16) для различных сигналов МНФ Аул ином и Сандбергом (1981). Например, рис. 5.3.6 иллюстрирует зависимость евклидова расстояния для двоичной ЧМНФ, как функцию индекса модуляции h при различном числе наблюдаемых

символьных интервалов N (N = 1,2,3,4).

Показана также верхняя граница dlih), определяемая (5.3.21). В частности.

Л/=1б

7 I-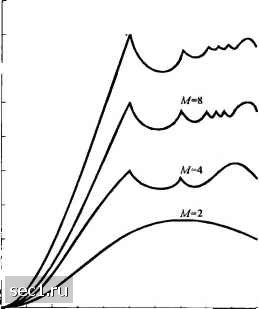

видим

, что когда /i-i, 5l{i) = 2, это

1 г

о 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

Рис. 5.3.5. Верхние границы dg как функция индекса модуляции дня сигнала МНФ с полным откликом и прямоугольным импульсом [Aulin nSundbetg(\9S4). © 1984, JoAm WileyLtd\

является тем же среднеквадратическим расстоянием, что для ФМ (двоичной или четверичной) с N = I.

С другой стороны, требуемое число интервалов наблюдения для ММС равно N = 2, из чего получаем 5,„(2) = 2. Следовательно, качество ММС с Ml 1110 сравнимо с качеством (двоичной или четверичной) ФМ, что мы видели раньше.

Из рис. 5.3.6 мы также замечаем, что оптимальный индекс модуляции для двоичной ЧМНФ равен /г-0,715, когда число интервалов наблюдения равно N = 3. Это дает

mm(715) = 2,43 или выигрыш в 0,85 дБ относительно ММС.

Рисунок 5.3.7 иллюстрирует зависимость евклидова расстояния от h для ЧМНФ сМ = 4 и числом интервалов наблюдения как параметра.

Также показана (штриховой кривой, которая не достигается) верхняя граница dl, рассчитанная по (5.3.22). Заметим, что 5,„ достигает верхней границы при некоторых значениях h при одинаковых N. В частности, отметим, что максимальная величина dl, которая получается при /i«0,9, приближённо достигается при iV = 8 наблюдаемых символьных интервалах. Действительный максимум достигается при Л = 0,914 с iV= 9. Для этого случая 5(0,914) = 4,2, что даёт выигрыш 3,2 дБ относительно ММС. Также отметим, что евклидово расстояние имеет минимумы при A = i, i,f,l и других значениях. Эти значения h называют слабыми индексами модуляции, и их избегают. Похожие результаты возможны для больших значений М, и их можно найти в работе Аулина и Сандберга (1981) и в публикациях Андерсона и др. (1986).