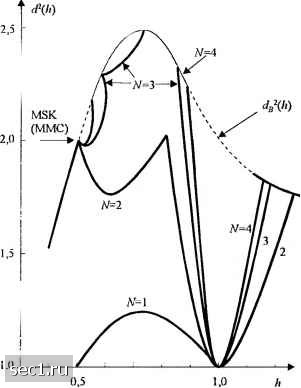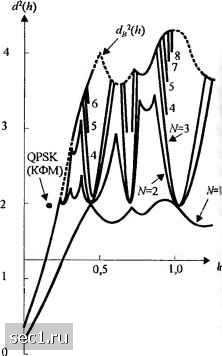Рис. 5.3.6. Минимальное евклидово расстояние

как функция индекса модуляции для двоичной ЧМНФ. Верхняя граница d. [Aulm nSundberg(1981), © 1981,IEEE]

Рис. 5.3.7. Минимальное евклидово расстояние как функция индекса модуляции для четверичной ЧМНФ. Верхняя граница dg. [Aulin и Sundberg (1981). © 1981, IEEE\

Большие выигрыши в качестве можно также достичь при МППО и для МНФ, используя сигналы с парциальным откликом. Например, граница расстояния dl{h) при парциальном отклике импульса приподнятого косинуса, определяемого выражением

2LT о

(l-cosj {Q<.t<LT),

(для других Т),

(5.3.23)

показана на рис. 5.3.8 для М-2.

Здесь заметим, что с ростом L параметр di также достигает больших значений. Ясно, что качество МНФ улучшается по мере увеличения коррелятивной памяти L, но следует также увеличить h для того, чтобы достичь больших значений dg. Поскольку больший индекс модуляции требует большей полосы частот (при фиксированном L), в то время как большая длина памяти L (при фиксированном И) требует меньшей полосы частот, то лучше сравнивать евклидово расстояние как функцию от нормированной полосы частот 2WT, где W - полоса с концентрацией 99% мощности, а 7 - битовый интервал. Рисунок 5.3.9 иллюстрирует этот вид сравнения с ММС, используемой как точка отсчёта (о дБ).

Из этого рисунка видно, что имеется выигрыш в несколько децибел при использовании сигналов с парциальным откликом и больших значений объема алфавита. Главная цена, которую нужно платить за этот выигрыш качества, - это экспоненциально растущая сложность в реализации декодера Витерби.

Л-г б г

4 дБ - 5 -

ЗдБ [- 4 -

2 дБ

ОдБ h 2 -

-ЗдБ - 1 L

- О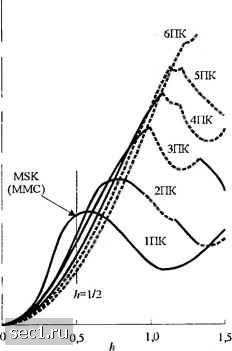

101gt0.5rf,J

Рис. 5.3.8. Верхняя граница dgaiui минимального

расстояния двоичной МНФ с парциальным откликом (импульс приподнятого косинуса) [simcberg (1986), © 1986,/£££1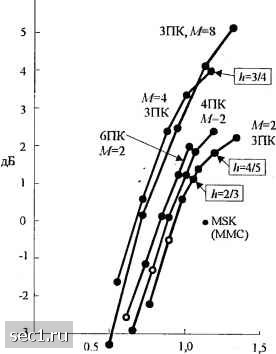

Рис. 5.3.9. Выирыш в полосе частот по мощности для сигнала МНФ с частичным отк.ликом (импульс приподнятого косинуса - ПК). W- полоса, содержащая 99 % мощности. [Sundberg {Ш6), © 1986,/£££]

Результаты качества, иллюстрируемые на рис. 5.3.9, показывают, что выигрыш относительно ММС в 3...4дБ можно легко получить без относительного расширения полосы частот, используя импульс приподнятого косинуса и МНФ с М = 4 и парциальным откликом. Хотя эти результаты получены для сигнальных импульсов приподнятого косинуса, похожие выигрыши можно достичь с другими огибающими импульсов при парциальном отклике. Подчеркнем, что этот выигрыш в ОСШ достигается введением памяти при модуляции сигнала и использованием памяти при демодуляции сигнала. Кодирование здесь не вносит избыточности. Фактически код здесь встраивается в модулятор, и декодирование решётчатого типа (Витерби) использует фазовые связи в сигнале МНФ.

Дополнительный выигрыш в качестве можно достичь введением дополнительной избыточности при кодировании и увеличением размера объема алфавита как средства, при котором сохраняется фиксированная полоса частот. В частности, МНФ с решётчатым кодированием, с использованием относительно простых свёрточных кодов, широко исследуется и много результатов имеется в технической литературе. Декодер Витерби для МНФ со свёрточным кодированием сегодня используют для учёта памяти, присущей и коду, и МНФ сигналу. Выигрыш качества порядка 4...6 дБ, обусловленный кодированием ММС с сохранением полосы частот, был продемонстрирован с комбинированием сверточного кодирования и МНФ. Обильные численные результаты для кодированной МНФ даны Линделлом (1985).

МНФ со многими индексами (multi-/j). Изменением индекса модуляции от одного сигнального интервала к другому можно увеличить минимальное евклидово расстояние

min между парами фазовых траекторий и таким образом улучшить выигрыш качества относительно МНФ с фиксированным индексом И. Обычно МНФ со многими индексами А использует фиксированное число Н индексов модуляции, которые меняются циклически в соседних сигнальных интервалах. Таким образом, фаза сигнала меняется кусочно-линейно.

Существенный выигрыш в ОСШ достигается использованием только небольшого количества различных значений h. Например, для МНФ с полным откликом (/, = 1) и Н = 2 можно получить выигрыш в 3 дБ относительно двоичной или четверичной ФМ. При увеличении Я до Я = 4 можно получить выигрыш в 4,5 дБ относительно ФМ. Выигрыш качества можно также увеличить с увеличением объема сигнального алфавита. Таблица 5.3.1 показывает выигрыш качества, достигаемый при М = 2, 4 и 8 для различных значений Я.

Таблица 5.3.1 Максимальные значения верхней границы dg для линейной МНФ с переменным индексом

Aulin и Sundberg (1982b)

На рис. 5.3.10 показана верхняя граница минимального евклидова расстояния для нескольких величин М и Н. По оси абсцисс отложено среднее значение h=Zh,.

Отметим, что основной выигрыш в качестве получается, когда Я увеличивается от Я = 1 до Я-2. Для Я>2 дополнительный выигрыш относительно мал для малых. величин

(/?,}. С другой стороны, существенный выигрыш качества достигается увеличением

объема алфавита М.

Результаты, показанные выше, имеют место для МНФ с полным откликом. Наверняка существует польза от МНФ со многими индексами h при парциальном отклике в попытке дальнейшего улучшения качества. Можно предвидеть, что такие схемы обеспечат дополнительный выигрыш качества, но имеющиеся численные результаты для МНФ со многими индексами h и парциальным откликом ограничены. Интересующемуся читателю рекомендуется статья Аулина и Сандберга (1982).

Многоамплитудная МНФ. Многоамплитудная МНФ (МАМНФ) является по существу схемой комбинирования амплитудной и фазовой модуляции, которая позволяет увеличить сигнальный алфавит относительно МНФ до другой размерности и таким образом достичь большей скорости передачи данных в частотно-ограниченном канале. Одновременно комбинирование AM с МНФ приводит к эффективной по полосе частот технике модуляции. Мы уже наблюдали спектральные характеристики МАМНФ в разд. 4.3.