2.1.2. Функции от случайных величин

Проблему, которая часто возникает в практических приложениях теории вероятности, можно сформулировать так. Дана случайная величина X, которая характеризуется своей ФПВ р(л-), и надо найти ФПВ случайной величины Y = g{X), где g()- некоторая заданная функция от X. Если преобразование от А к 7 взаимно однозначное, определить р{у) относительно просто. Однако, если преобразование не является взаимно

однозначным, как в случае, например, когда 7 = А", мы должны быть более внимательны в определении р{у).

Пример 2.1.1. Рассмотрим случайную величину У, определённую как

Y=aXb, (2.1.39)

где анЬ- константы. Мы предположим, что а>0. Если а<0, подход тот же (см. задачу 2.3). Заметим, что это преобразование, иллюстрируемое рис. 2.1.4, (а), является линейным и монотонным.

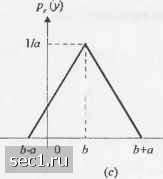* у

Рис. 2.1.4 Линейное преобразование случайной переменной и пример соответствующих ФПВдляXuY

Пусть /\(x) и FJy) определяют ИФР для Z и К соответственно. Тогда

Fy{y) = P(Y < у) = F(ciX + Ь <у)= Р

\ Ct )

My Ь) а

p{x)dxF

\ а J

Дифференцируя (2.1.40) по>, получаем зависимость между соответствующими ФПВ

(у-Ъ

Рг(у) = -Рл а

(2.1.40) ;ими ФШ (2.1.41)

Таким образом, (2.1.40) и (2.1.41) определяют ИФР и ФПВ случайной величины У через ИФР и ФПВ случайной величины Адля линейного преобразования (2.1.39). Чтобы проиллюстрировать это преобразование для определённой ФПВ р{х), рассмотрим пример распределения на рис. 2.1.4,(6). Полученная ФПВ для преобразования (2.1 39) показана на рис. 2.1,4,(с).

Пример 2.1.2. Рассмотрим случайную величину 7, определённую как

У-аХ+Ь,а>0. (2.142)

Как в примере (2.1.1), преобразование X в К взаимно однозначное, следовательно.

Чтобы избежать ошибки при замене переменных использованы индексы для соответствующи.\ ФПВ и ИФР.

Fy(y) = P(Y<y) = P(aX+b<y) = P X<

(у-ЬЛ

\ a j

Дифференцирование (2 1 43) no; даёт соотношение между двумя ФПВ

3ab-b)laY

у-ЬЛ

(2 1.43)

(2.1.44)

Пример 2.1.3. Случайная величина У определена как

Y = aX-+b,a>0. (2.1.45)

В отличие от примеров (2.1.1) и (2.1.2), связь между и У, иллюстрируемая рис. 2.1.5, теперь не взаимно однозначная. Чтобы найти ИФР для К, заметим, что

Следовательно,

Fyiy) = Р{У <у) = Р(аХ- +Ь<у) = Р

[y-b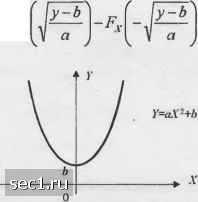

(2.1.46)

Рис. 2.1.5. Квадратичное преобразование случайной переменной .V

Дифференцируя (2.1 46) по у, мы получим ФВП У через ФВПХв виде

(у-Ь)/а

(2 1 47)

(у-Ь)/а\ 2а[(у-Ь)/а\

Для примера (2.1.3) мы замечаем, что уравнение g(x) = ax+b=y имеет два вещественных решения:

а V а

и что Ру(у) содержит два слагаемых, соответствующих этим двум решениям:

\х,-(у-Ь)/а

Рг(у) =

X, ={у-Ь)1а

(2.1.48)

где gix) означает первую производную от (х) по х

В общем случае предположим, что х\, Хг, х« являются вещественными корнями уравнения gix) = у. Тогда ФПВ для случайной величины Y=g(X) можно выразить так

(2.1.49)

Priy)>

где корни X,, /=1, 2, .. , w являются функциями от у. .16

Теперь рассмотрим функции от многомерных случайных величин Предположим, что А,, /=1, 2, /7, являются случайными величинами с СФПВ p.\(xi,X2, ...,х„) и что К,, /=1,2, ..., н - другой ряд случайных величин, связанных с X, функциями

Y,=gXX„X„...,X„l /-1.2,...,». (2.1.50)

Считаем, что g:(X\, Х2. Х„), /=1, 2, н, являются однозначными обратимыми функциями с непрерывными частными производными. Под «обратимыми» мы понимаем то, HToXj, 2, можно выразить как функции от У,-, /-1, 2, в форме

.=g:\y,y-xi /=.и,...,«, (2.1.51)

причём обратные функции также считаются однозначными с непрерывными частными производными. Задача сводится к определению СФПВ К,, /=1, 2, ...,«, т.е. ру()и)2,- J-v), через заданную СФПВр\{х], Х2, ..., х„).

Чтобы найти нужное соотношение, положим, что Rx означает область в -мерном пространстве случайных переменных А,, /=1, 2, ..., , и что является областью взаимнооднозначного отображения в Rx, определенной функциями Y,-g,(Xi, Х2, ...,Хп).

Очевидно, что

] jPr(yuy7> -yMiyi-dyn = /...j/.v(x„X3,...,x„)a?Y,£/Y,...afY„. (2.1.52)

Путем замены переменных в многомерном интеграле в правой части (2.1.52) по формулам

X. giiyi.y2,-,yJ-g., / = 1.2,..., .

получаем

(2.1.53)

где./-якобиан преобразования, равный определителю

dg: dg::

(2.1.54)

Sy., dy„ dy„

Следовательно, искомое соотношение для СФПВ всех Y,, i=\, 2, ..., ,

Рг(УиУ2<-,Уп)-Рх(> =g\x,=g:\...,x„ =gjp\. (2.1.55)

Пример 2.1.4. Важное функциональное соотношение между двумя рядами -мерных случайных величин, которое часто встречается на практике, - линейное преобразование

.=ZSy = 1.2, (2.1.56)

где {а,,} - постоянные. Можно воспользоваться матричной формой преобразования

Y = AX, (2 1.57)

где X и Y являются -мерными векторами, а А - матрица размером пхп . Предположим, что матрица А - невырожденная. Тогда матрица А обратима, и

X = A-Y. (21.58)

Эквивалентная скалярная запись