расширения времени корреляции на три символа. Дальнейшее расширение интервала корреляции ведет к относительно малому дополнительному выигрышу.

Похожие результаты получены посредствам большего объёма алфавита. Например, рис. 5.3.13 и 5.3.14 иллюстрируют улучшение качества четырехпозиционной и восьмипозиционной ЧМНФ соответственно. Индексы модуляции, данные на этих графиках, такие, что они минимизируют вероятность ошибки на символ.

10-"

4 б 8 10 ОСШ на бит, Yi. дБ

14 О

4 6 8 10 ОСШ на бит, Y4.flB

Рис. 5.3.13. Характеристики качества четверичной ЧМНФ при когерентном детектировании

Рис. 5.3.14. Характеристики качества восьмеричной ЧМНФ при югерентном детектировании

Вместо осуществления когерентного детектирования, которое требует знания фазы несущей фо, мы можем предположить, что фд равномерно распределена на интервале 0...27I, и выполнить усреднение по фазе при получении величин для решения. Так осуществляется когерентное интегрирование (взаимная корреляция) по п = D + 1 сигнальным интервалам, но выход корреляторов детектируется по огибающей. Эту процедуру называют некогерентным детектированием ЧМНФ. В этой схеме детектирования достигается оптимизация качества путем выбора нечетного п и выполнения решения по среднему символу последовательности из и символов. Численные результаты для вероятности ошибки при некогерентном детектировании ЧМНФ похожи на результаты иллюстрированы выше для когерентного детектирования. Это значит, что выигрыш в 2...3 дБ в качестве достигается путем увеличения интервала корреляции от A?=l до п-3 идо п-5.

5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ

В этом разделе рассмотрим синтез оптимального приёмника для модулированных сигналов, когда фаза несущей неизвестна в месте приёма и не делается никаких попыток оценить ее значение. Неопределенность фазы несущей принимаемого сигнала может быть обусловлено одной или большим числом причин. Первое: генераторы, которые используются в передатчике и приёмнике для генерирования сигналов несущей, обычно не имеет фазового синхронизма. Второе: время задержки при распространении сигнала от передатчика к приёмнику в общем не известно точно. Чтобы рассмотреть этот вопрос, положим, что переданный сигнал

= Re[/)e"<

проходит через канал с временем запаздывания to, так что принимаемый сигнал л(/ - /„) = Re[g(/ - /о)е"(-°] = Rc[g(f - /„)e-«e . Фазовый сдвиг несущей, обусловленный временем задержки , равен

Ф--2Я/Л.

Заметим, что большие изменения в фазе несущей могут возникнуть при относительно малых изменениях времени задержки. Например, если частота несущей /=1МГц, неопределенность или изменения во времени распространения на 0,5 мкс вызовут неопределенность фазы к радиан. В некоторых каналах (например, радиоканалах) время распространения сигнала от передатчика к приёмнику может изменяться быстро и очевидно случайным образом, так что фаза несущей принимаемого сигнала меняется очевидно случайным образом.

При отсутствия знания фазы несущей, мы можем трактовать этот параметр сигнала как случайную величину и определять при этом оптимальный приёмник для извлечения переданной информации из принятого сигнала.

Сначала рассмотрим случай двоичных сигналов и затем рассмотрим М позиционные сигналы.

5.4.1. Оптимальный приёмник двоичных сигналов

Рассмотрим двоичную систему связи, которую используют для передачи информации двух модулированных по несущей сигналов 5,(/) и s{f), где

„,()-Rek(/)e

2, 0<t<T,

а .V, „,(/), m = 1, 2, - эквивалентные низкочастотные сигналы. Считается, что два сигнала имеют равные энергии

и они характеризуются комплексным коэффициентом корреляции

sl{l)s,XJ)di.

(5.4.1)

(5.4.2)

(5.4.3)

Считается, что принимаемый сигнал отличается от переданного случайной фазой и подвергается воздействию аддитивного шума

(5.4.4)

n{t) = Ке{[и,(0 + А(/)У"} = Re[2(/)e Таким образом, принимаемый сигнал можно выразить так:

K) = Re{[5,„,We*+z(/)]e"-},

(5.4.5)

•/W = J/)e*+z(/), 0</<Г, (5.4.6)

- эквивалентный низкочастотный принимаемый сигнал. Этот принимаемый сигнал теперь проходит через демодулятор, отсчёт которого при / = Г подается на детектор.

Оптимальный демодулятор. В разд. 5.1.1 мы показали, что, если принимаемый

сигнал коррелируется с набором ортонормированных функций {/,(/)), на которые

натянуто пространство сигналов, выходы набора корреляторов обеспечивают набор достаточных статистик для детектора с тем, чтобы сделать решение, которое \ минимизирует среднюю вероятность ошибки. Мы также показали, что набор согласованных фильтров может заменить набор корреляторов.

Похожее ортонормированное разложение можно выполнить по отношению к принимаемому сигналу с неизвестной фазой несущей. Однако математически удобнее иметь дело с эквивалентным низкочастотным сигналом и. выполнить сигнальные корреляторы или согласованные фильтры по отношению к эквивалентным низкочастотным сигналам.

Для конкретности: импульсная характеристика фильтра, согласованного с комплексным эквивалентным низкочастотным сигналом .?,(/), 0<i <Т, определяется так (см. задачу 5.6):

h,{i) = s;{T-t), (5.4.7)

а выход такого фильтра в момент t = Т равен.

j\s,{tfdt = 2fS, (5.4.8)

где 8 - энергия сигнала. Аналогичный результат получается, если сигнал s,{t) коррелируется с s,{t), а коррелятор стробируется в момент времени t - Т. Следовательно, оптимальный демодулятор для эквивалентного низкочастотного принимаемого сигнала s,{t) в (5.4.6) можно реализовать двумя согласованными фильтрами, работающими

параллельно, один согласован с 5„(/), а другой с (/). Он показан на рис. 5.4.1. Выходы согласованных фильтров или корреляторов в точках отсчёта являются двумя комплексными числами

fn.=r+Jr, /и =1,2. (5.4.9)

Предположим, что передаётся сигнал 5, (t). Тогда легко показать (см. задачу 5.35), что

r = 28 cos ф + /г, + j{2% sin ф + «, J,

= 28рсо5(ф + а(,)+И2.+Х2рЩф + °о) + «1.), "

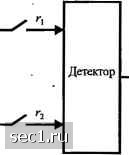Выходное решение

Рис. 5.4.1. Оптимальный приёмник для двоичных сигналов