(5.4.41)

p = p{r,<r„r,<r„...,r<r,) =

= Jр(/г, < < Л„...,Лл. < = x)p)dx. Поскольку случайные величины r, т = 1,Ъ,...,М, статистически независимы, совместная вероятность в (5.4.41) определяется произведением М- \ идентичных членов:

Рс-\\Р[ <.к =Г (5.4.42)

p[r, <Л,К =х) = £,Да-2)2 =l-e-/ (5.4.43)

Степень М -1 от (5.4.43) можно выразить, пользуясь биномом Ньютона, так:

\ п J

(5.4.44)

Подставив этот результат в (5.4.42) и интегрируя по х, получаем для вероятности правильного решения

/1=0

(5.4.45)

где JNq - ОСШ на символ. Тогда вероятность ошибки на символ = 1 - Р равна

/7 + 1

{n + \)N,

(5.4.46)

где EJNq - ОСШ на бит.

Для двоичных ортогональных сигналов (М = 2) (5.4.46) приводится к простому виду

Р=\е\ (5.4.47)

Для М > 2 мы можем вычислить вероятность ошибки на бит, используя соотношение

(5.4.48)

которое было установлено в разд. 5.2. Рисунок 5.4.5 показывает вероятность ошибки на бит как функцию ОСШ на бит y, для М = 1, 4, 8, 16 и 32. Для случая когерентного детектирования М-позиционных ортогональных сигналов (см. разд. 5.2.2) мы видели, что для любой заданной вероятности ошибки ОСШ на бит уменьшается по мере роста М В гл.7 будет показано, что в пределе, когда М-хх) (или Л =*1о§2 М-> оо), вероятность

ошибки на бит Р можно сделать сколь угодно малой при условии, что ОСШ на бит превышает предел Шеннона -1,6 дБ. Цена роста М - увеличение полосы, требуемой для передачи сигнала. Для М-позиционной ЧМ разнос частот между соседними частотами равен Д / = 1 / 7" для ортогональности сигналов. Полоса частот, требуемая для М сигналов, W = МА f = М IT. Таким образом, битовая скорость R = k IT, где к = log М. Следовательно, отношение битовой скорости к полосе равно

R log-; М

w~ м

(5.4.49)

Этот результат впервые получил Л.М. Финк в 1957 г. [23] (прп).

10-»

10-"

10-5

io-«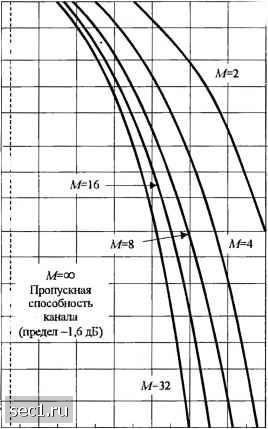

2 4 6 8 ОСШнабит, у.дБ

Рис. 5.4.5. Вероятность ошибки на бит для некогерентного детектирования ортогональных сигналов

5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей

В этом разделе рассмотрим качество детектора огибающей для двоичных коррелированных сигналов равной энергии. Если два сигнала коррелированы, на вход детектора поступают комплексные величины, определенные (5.4.10). Предположим, что

и к

детектор выносит свои решения на основе огибающих

коррелированы (статистически зависимы). Собственные ФПВ для 7?, = распределены по Раису, и их можно выразить так:

которые теперь

Ля.)-

(5.4.50)

(К,>0),

О к<о),

/н = 1, 2, где Р, = 2g и Р2 = 28р получены в предположении, что был передан сигнал s{t).

Поскольку Л, и i?2 статистически зависимы, как следствие неортогональности сигналов, вероятность ошибки можно найти, вычислив двойной интеграл

р, = p{r, > л;) = jjjjp(x„ X2>/V-3, (5.4.51)

где p{xi,x-,) - совместная ФПВ огибающих Л, и R-,. Это исследование было впервые

вь полнено Хелстромом (1955), который определил совместную ФПВ Л, и и рассчитал

двойной интеграл в (5.4.51).

Альтернативный подход базируется на наблюдении, что вероятность ошибки можно выразить так;

р, = p(r, >R,) = p(r- >R;)= р(р; -Rf > о). (5.4.52)

Но - Л," - это частный случай общей квадратичной формы комплексных гауссовских случайных величин, рассмотренных в приложении В. В этом частном случае вероятность ошибки можно выразить в виде

n-QM-feiM), (5.4.53)

(5.4.54)

OX<,b) это 0-функция Map кума, определенная (2.1.123), и 1{х) - модифицированная функция Бесселя нулевого порядка.

Вероятность ошибки р,, иллюстрируется на рис. 5.4.6

10 2

S 10"

J 10 II 12 13 14 15 16 17 И

ОСШ на бит. Yj. дБ Рис. 5.4.6. Вероятность ошибки для некогерентного детектирования

для нескольких значении

. Вероятность минимизируется, когда р = О, т.е. когда

С)1гналы ортогональны. В этом случае а = 0, Ь = Je/Nq , и (5.4.53) даёт

-> с

(5.4.55)