"2(0

из(0

«4(0

Ансамбль I

",(0

",(0

"2(0

"2(0

1 2

"з(0 о

"4(0

12 3;

Ансамбль II

12 3 4

"4(0

Vl/2 а

-л1\/2 а

л11/2А О

1 2

t

Vl/2/I

у1\/2а о

Ансамбль Ш

Рис. P5.I3

с) Для сигналов ансамбля 1 определите среднюю вероятность ошибки, если сигналы детектируются когерентно.

(1) Для сигналов ансамбля II дайте объединённую фаннцу для вероятности ошибки на символ, если

детектирование выполняется когерентно (i) и некогерентно (ii). с) Возможно ли некогерентное детектирование для сигналов ансамбля III. Объясните. о Какой сигнальный ансамбль или сигнальные ансамбли вы выберете, если желаете достичь

отношения битовой скорости к полосе частот r/jv не менее 2. кратко объясните ваш ответ. 5.14. Рассмотрите четыре.хпозиционную (М = 4) систему связи, которая передает каждые Т секунд один из четыре.ч равновероятны.\ сигналов s(t)-s(t),S2(t)-s2{t). Сигналы .Sj(f) и Sjit) ортогональны и с равной знергией. Аддитивный шум гауссовский белый с нулевым средним и автокорреляционной функцией (])„(т)= Ло5(т). Демодулятор состоит из двух фильтров, согласованных с и и их выходы в

отсчётных точках равны f/, п U.

Детектор основывает свое решение на правиле

С/, > С/, (О, f/, <-р.] (/),

о(0 i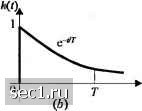

Рис. Р5.15

Поскольку сигнальный ансамбль биортогонален, вероятность ошибю! равна (}-Р,), где опреде.ояется (5.2.34). Выразите эту всроетность ошибки через одномерный интефал и затем покажите, rгo вероятность ошибки на символ для биортогонального сигнального ансамбля из Л/ = 4 сигналов идeнтишa той, которая определяет четырс.\()><1знлю ФМ. Подсказка: замена переменных f/, и на U\=U+U2 и =11-11., J прощает задачу.

5.15. На в.ход полосового фильтра поступает сигнал s{t).

где V(/) - прямоугольный импульс, показанный на рис. Р5.15 (а).

a) Определите выход y{t) полосового фильтра д.ля всех / > О, если импульсная характеристика этого фильтра

где /(г) - экспонента, показанная на рис. Р5.15 (Ь).

b) Нарисуйте выход эквивалентного низкочастотного фильтра.

c) В каких точках возьмёте отсчёты выхода фильтра, если желаете иметь максимальный выход в точках отсчёта? Чему равны ъе,ят\\ны максимальных отсчётов?

d) Предположите, что .v(/) суммируется с АБГШ

где Ф--(т) A,S(t). в точках отсчёта, определённых в п. (с), на отсчёты сигнала теперь на1сладываются

шумовые гауссовские слагаемые.

e) Каково отношение сигнал/шулг у по отсчётам выхода?

О Определите отношение сигнал/шулг, когда h{t) - хараетеристик! фильтра, согласованного с и сравните эти результаты с вели»ганой у , полученной в (е). 5.16. Рассмотрите BocbNmTOHCHHoe сигнальное

С0{всздие на рис. Р5.16. i

a) Ближайшие соседние точки в снгнальнол[ сошсздии 8-КАМ наход)гтся на расстоянии А единиц. Определите радиусы а II /) внутренней и внешней окруишости.

b) Соседние сигнальные точки в созвездии 8-ФМ находятся на расстоянии А единиц. Определите радиус г окруясности. Определите среднюю переданнуто лющность ДЛ51 двух сигнальных созвездий и сравните обе лющности.

8-ФМ

8-КАМ

Рис. Р5.16

Каков относительный выигрыш по лющности одного созвездия относительно другого? (Предположите, что все сигнальные точи! равновероятны.)

5.17. Расслютр1гге 8-точсчное сигнальное созвездие КАМ, покгзаннос на рис. Р.5.16.

a) Возлюжно лн сопоставнть три бита данных каждой точке сигнального созвездия так, 1ггобы ближайшие (соседние) точки отличались бы только в одном битовом силшоле?

b) Определите скорость передачи символов, если желательная битовая скорость 90 Мбит/с.

5.18. Предположим, что двoишaя ФМ используется д.лл передачи информации по каналу с АБГШ со спектральной плотностью мощности "сП/д-ъ. Энергия передаваемого сигнала 4, =\АТ, где Т-битовый интервал, .1-амплитуда сигнала. Определите амплитуду сигнала, требуемую для достиженш! вероятности ошибки Ю"*", если скорость передачи данных равна а) 10 кбит/с: Ь) IOO кбит/с и с) 1 Мбит/с.

5.19. Расслютрите детсетор сигнала со в.ходом r-+A+ii. где +А и А появляются с равной вероятностью, а шулювое слагаемое п .характеризуется лапласовской ФПВ, показанной на рис. Р5.19.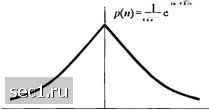

Рис.Р.5.19.

a) Определите вероятность ошибки как функцию от параметров А и а .

b) Определите ОСШ, требуемое для достижения вероятности ошибки 10". Каково требуемое ОСШ по сравнению с результатом для гауссовской ФПВ?

5.20. Рассмотрите два 8-точечных сигнальных созвездия КАМ, показанных на рис. Р5.20.

(о) Ф)

Рис. Р5.20

Минимальное расстояние между соседними точками равно 2 А . Определите среднюю передаваелгую мощность для каждого созвездия, предполагая, что сигнальные точки равновероятны. Какое созвездие эф()ективнее по мощности?

5.21. Для сигнального созвездия КАМ, показанного на рис. Р5.21, определите оптимальные границы решения детектора, предполагая, что ОСШ достаточно велико, так чго ошибочные переходы имеют место только между соседними точками.

5.22. Постройте код Грея для сигнального созвездия 16-КАМ, показанного на рис. Р5.21.

5.23. Квадратурные несущие coslnfj и sinlnfj

3 5 используются для передачи цифровой информации по каналу с АБГШ при двух различных скоростях передачи данных 10 кбит/с и 100 кбит/с. Определите относительные амплитуды сигналов для двух несущих так, чтобы /Aj для двух каналов были бы одинаковыми.

Рис. Р5.21

5.24. Три сообщения т,, /Hj и нужно передавать по каналу с АБГШ со спектральной плотностью .мощности irNff. Сообщения определяются так:

fl (0<f<r), ~[0 (для других/),

1 {0<1<Т),

ф) = -ф) = \-\ (tr</<r).

О (для других

a) Какова размерность пространства сигналов?

b) Найдите подходящий базис для пространства сигналов. (Подсказка: вы можете найти базис без использования процедуры Грама-Шмидта.)