c) Начертите сигнальное созвездие для этой задачи.

d) Рассчитайте и постройте оптим- льные области решения R, и Л3.

e) Какое из трех сообшений более уязвимо для пол:ех и почему? Другими словами, чья условная

вероятность /(ошибка передан ш,), / = 1,2,3 , больше?

5.25. Если аддитивный шум на в.чодс демоду.щггора окрашенный, фильтр, согласованный с сигналом, больше не максимизирует выходное ОСШ. В этом случае мы можем рассмотреть использование предварительного фильтра, который «обеляет» окрашенный шум. За этим предварительным фильтром след)ет фильтр, согласованный с профильтрованным полезным сигналом. С учетом сказанного рассмотрите схему, показаннто на рис. Р5.25.

К/)=5(/)+«(0.

(О - OKpiOUCH-

ный ш\м

Обс115иощии фильтр

ФИЛЬТ}!,

согласованный с s[l)

Отсчет в момент/= Г

Детектор

Рис. Р5.25

a) Определите частотную характеристику предварительного (1)ильтра, который обеляет шум.

b) Определите частотную характеристик} фильтра, согласованного с .v (/).

c) Расслютритс каскадное соединение предварительного фильтра и согласованного фильтра i лк единый «обобщсннь й согласованный фильтр». Какова частотная характеристика этого ()ильтра?

d) Определите ОСШ h;i входе детектора.

5.26. Расслютритс ци()ров)ю систему связи, которая передает информацию посредством КАМ через стандартный телефонный канал со скоростью 2400 симв./с. Аддитивный шум считается гауссовским и белым.

a) Определите \ jN , требуемое для достижения вероятности ошибки 10" при передаче 4800 б1гт/с.

b) Повторите (а) для скорости 9600 бит/с.

c) Повторите (а) для скорости 19200 бит/с.

d) Каше за1с.лю юния вы сделаете из этих результатов?

5.27. Рассмотрите чстырехфазное и восьмифйзное сигнальные созвсздшк показанные на рис. Р.5.27.

Л/ 8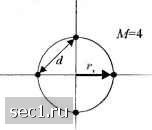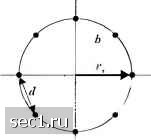

Рис Р5.27

Определите радиусы r и г,. окружностей так, чтобы расстояние между ближайшими точками в двух

созвездиях бьшо равно d. Исходя из этого результата, определите требуемую дополнительную энергию для 8-ФМ, чтобы достичь той же вероятности ошибки, кяк при 4-ФМ, примелг вероятность ошибки определяется ошибками при выборе соседн! х точек созвездия.

5.28. Цифровая информация передается люду.ляцисй несущей по каналу с АБГШ с полосой 100 idTa а .V, = 10 ° Вт/Гц. Определите максимальнуло скорость передачи по каналу при четырёхфазной ФМ, двоичной ФМ и четырехпозиционной ортогональной ЧМ с нскогерентныл детектированием.

5.29. В сигнале ММС начальное состояние фазы равно О или л рядиан. Определите финальное состояние фазы для следующих четырех входных пар дгшных; а) 00; Ь) 01; с) 10; d) II.

5.30. Сигнал ЧМ с непрерывной фазой с Л = представлен так

соз2лЛ/± Ssinf

s.u\2nfj. О < / < 27; ,

где знаки ± зависят от передаваемых информационных битовых символов.

a) Убедитесь, «гго этот сигнал имеет постоянную амплитуду.

b) Нарисуйте блок схему модулятора для синтеза сигнала.

c) Нарисуйте блок-схему демодулятора и детектора для извлечения информации.

5.31. Нарисуйте фазовое дерево, решётку состояний и диаграмму состояний для МНФ с парциальным откликом при Л = и

1/4Г (0</2Г), О (для других/).

5.32. Определите число финальных состояний фазы на диаграмме решётки состояний для (а) двошой ЧМНФ с полным откликом с Л = или и (Ь) двоичной ЧМНФ с парциальным откликом с 1 = 2 и

Л = т или i.

5.33. Рассмотрите биортогональный ансамбль с Л/ = 8 сигнальными точками. Определите объединённзю верхнюю границу для вероятности ошибки на символ как функцию /jVq . Сигнальные точки считаются априори равновероятными.

5.34. Рассмотрите М -позиционную цифровую систему, где Л/ = 2. а jV - размерность пространства сигналов. Предположим, что точки М сигнальных векторов лежат на вершинах гиперкуба, который центрирован относительно начала координат. Определите среднюю вероятность ошибки на символ как функцию от isjnq , где - энергия на символ, N, - спектральная плотность мощности АБГШ, а все

сигнальные точки равновероятны.

5.35. Рассмотрите сигнал

(0=1;,р(-*7;).

где pit) - прямоугольный импульс единичной амплитуды и длительности . Коэффициенты {с J можно

где элементы с, = ±1. Покажите, пo фильтр.

С,С2...С„

рассматривать как кодовый вектор С = согласованный с сигналом s{t), можно реализовать как каскад из фильтра, согласованного с p{t). и фильтра дискретного времени, согласованного с вектором С . Определите величину выхода согласованного фильтра в точках отсчётов / = iT.

5.36. Речевой сигнал стробнруется со скоростью 8 кГц, логарифмически сжимается и кодируется в ИКМ-формат с использованием 8 бит/отсчёт. Данные ИКМ передаются через базовый канал с АБГШ посредством М -уровневой AM. Определите полосу частот, требуемую для передачи, когда (а) М -4, (Ь) М = 8. (с) Л/ = 16.

5.37. Матрица Адамара определяется как матрица, чьи элементы равны ±1 и чьи вектор- строки попарно ортогональны. Для случая, когда и равно степени 2, пхп матрица Адамара конструируется посредством рекчррентной процедуры:

а) Пусть С, означает ;-ю строку пхп матрицы Адамара, как она определена выше. Покажите, что сигналы, образованные так:

ортогональны, где p{t) - произвольный импульс, определённый на временном интервале 0<.t<T.

b) Покажите, что согласованные фильтры (или взаимные корреляторы) для п сигналов {sj{t)} могут бьггь реализованы посредством единственного фильтра (или коррелятора), согласованного с импульсом p{t), за которым следуют п взаимных корреляторов, использующих кодовые слова {С,}.

5.38. Дискретная последовательность

к = -jfk + Я = 1,2,...и,

представляет выходную последовательность отсчётов демодулятора, где = ±1 - элементы одного из двух возможных кодовых слов с, = [1I...III...1] и Cj = [ll...l-l-l...-l]. Кодовое слово Cj имеет w элементов +1 и

п - w элементов -1, где w - некоторое положительное целое число. Шумовая последовательность [п,}

является гауссовской и белой с дисперсией а".

a) Каков детектор максимального правдоподобия для дву.х возможных передаваемых сигналов?

b) Определите вероятность ошибки как функцшо параметров (a.E.w).

c) Какова величина w , которая минимизирует вероятность ошибки?

5.30. Полуште выходы г, и дву.х корреляторов, показанных на рис. 5.4.1. Считайте, что передаётся сигнал хц (/) и что

,(/) = .,.(/VUz(/), где z(/)= л(/) + jii(t) - аддитивный гауссовский шум.

5.40. Определите ковариаций и дисперсии гауссовских случайных шумовых величин пс>>ъ. •wis (5.4.15) и их совместную ФПВ.

5.41. Получите выходы согласованного фильтра, определенные (5.4.10).

5.42. В двоичной системе AM с пассивной паузой два возможных сигнала

s{f) = (\Q<t<Tb.

coslnfJ,Q<t<Tb.

Соответствутощие принимаемые сигналы

г(/) = (4 0 5/<Гь,

КО - MWJ+Ф)+«().о т,.

где ф - фаза несущей, а /?(/) - АБГШ.

a) Н;1рис>йте блок-схему приёмник:) (демоду.лятора и детектора), который реализует некогерентное (по огнбгиощей) детектирование.

b) Определите ФПВ для двух участвующих в решении на вы.ходе детектора велшн, соответствующих двум возможным принятым сигнала

c) Определите вероятность ошибки детектора.

5.43 В двухфазной ДФМ принимаемый сигнал на одном сигнальном интервале используется как onopHbiii (эталонный) для принимаемого сигнала на следующем сигнальном интервале. Решение принимается по величине

представляют комплексный выход фильтра, согласованного с переданным сигналом м(/), Л/. -комплексные гауссовские величины с нулевым средним и статистически независимыми компонентами.

a) Написав 1 Л\. -1- JY . покажите, гтo D эквивалентно

D - [(А-„, +-V„ ,)f +[(Г„ +у„, ,)]- -x„, ,)f-l{Y„. -r„,.,)f.

b) Для математического удобства предположите, rгo 9. - 9 ,.

Покажите, что случайные величины f/, f/j, 17 - статистичес1си независимые гауссовские величины, где U, = (х„, + Jf,, ,), U, = (У„, + U, = i(„, - Х„, ,), = {Y„ - У„ ,).

c) Введите случайные величины =U+11 и W2=Ul +11. Тогда решающее правило детектора

D - (F, Определите ФПВ для и fF..

"О"

d) Определите вероятность ошибки Р,:

Рь = P{D <0)= P((F, - IFj < о) = Р(ГК, > w, w, )p{w )dw .