так что квадратурные компоненты njj) и nj(f) имеют точно такие же статистические характеристики, как x(t) и y(t).

Если s(f) +n(t) умножается на выход ГУН, а слагаемым с удвоенной частотой несущей можно пренебречь, на вход петлевого фильтра действует защумлённый сигнал

e(t) = 8шАф+«()8тЛф-лД/)со8Аф А зшАф+лгД/), (6.2.27)

где, по определению, Аф = ф - ф - фазовая ошибка. Таким образом, мы имеем эквивалентную модель для ФАП с аддитивным шумом, как показано на рис. 6.2.6.

©

ДФС)

Рис. 6.2.6. Эквивалентная модель замкнутой петли ФАП с аддитивным шумом

Если мощность Р = \а1 приходящего сигнала намного больше, чем мощность шума, мы можем линеаризовать ФАП и, таким образом, легко определить влияние аддитивного шума на качество оценки ф. При этих условиях модель линеаризованной ФАП с аддитивным шумом иллюстрируется рис. 6.2.7.

",(0

дф(0

Рис. 6.2.7. Линеаризованная модель замкнутой петли ФАП с аддитивным шумом

Заметим, что параметр усиления можно нормировать к 1, выполнив умножение шумовых слагаемых на 1 / Д,; тогда шумовая компонента становится равной

(Л ЛА АЖ

«2 (/) = ~- sm Аф - cos Аф .

(6.2.28)

Поскольку шум nit) на входе петли является аддитивным, дисперсия фазовой ошибки Дф, которая является также дисперсией фазы выхода ГУН, равна

(6.2.29)

где Я,,, - односторонняя эквивалентная шумовая полоса петли, определяемая (6.2.22). Заметим, что Оф-просто отношение суммарной мощности шума в полосе ФАП к А. Следовательно,

a5 = l/Yi, (6.2.30)

где у 1 определено как отношение сигнал/шум

ОСШу.Тт!-. (6.2.31)

Выражение для дисперсии ст ошибки фазы на входе ГУН относится к случаю, когда

ОСШ достаточно велико, так что приемлема линейная модель ФАП. Точный анализ нелинейной модели ФАП поддается математической обработке, когда G{s) -1, что относится к петле первого порядка. В этом случае можно получить ФПВ для фазовой ошибки (см. Витерби, 1966), и она имеет вид

(6.2.32)

где 7-0CШ, даваемое (6.2.31) с Д,, которая является соответствующей шумовой полосой петли первого порядка, а - модифицированная функция Бесселя нулевого порядка.

Из выражения для /Аф) можно получить величину дисперсии для фазовой ошибки для петли первого порядка. График дан на рис 6.2.8 как функция от \/у[. Для сравнения показан результат, полученный для линеаризованной модели ФАП. Заметим, что дисперсия для линейной модели тесно примыкает к точной дисперсии для Yi>3. Следовательно, линейная модель подходит для практических целей.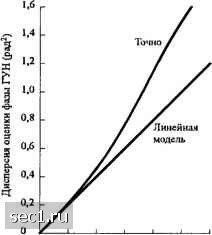

о 0,2 0,4 0.6 0.8 1,0 1,2

Рис. 6.2.8. Сравнение дисперсии фазы на вььходе ГУН при точной

и приближённой (линеаризованной) модели ФАП 1 порядка. [А.Дж.Витерби, Принципы когерентной связи; © 1966 McGraw-Hill Book Company]

Приближённый анализ статистических характеристик фазовой ошибки для нелинейной ФАП также проведён. Особую важность имеет переходный процесс ФАП на начальной стадии. Другая важная проблема - поведение петли при низких ОСШ. Известно, например, что, когда ОСШ на входе ФАП понижается ниже определенной величины, наблюдается быстрое ухудшение качества ФАП. Начинаются срывы синхронизма, приводящие к импульсному шуму, проявляющемуся как щелчки, который приводит к потере качества ФАП. Результаты по этим вопросам можно найти в книге Витерби (1966), Линдсея (1972), Линдсея и Саймона (1979), Гарднера (1979) и в некоторых статьях Гупта (1975), Линдсея и Чай (1981).

До сих пор мы рассматривали оценку фазы несущей, когда несущая не модулирована. Ниже мы рассмотрим восстановление фазы несущей, когда несущая несёт информацию

6.2.4. Петли, управляемые решениями

Когда сигнал i{t,) несёт на себе информационную последовательность [IJ, встаёт

проблема максимизации (6.2.9) или (6.2.10). В этом случае мы можем принять один из двух подходов: или мы предположим, что {/„} известно на приёме, или мы будем трактовать {/„} как случайную последовательность и выполним усреднение по её статистике.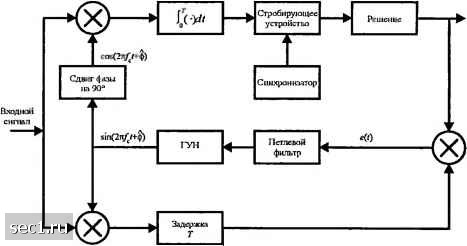

Вылод

Рис. 6.2.9. Восстановление несущей в системе ФАП с обратной связью по решению

При оценивании параметра в условиях управления решениями мы считаем, что информационная последовательность {IJ на интервале наблюдения оценена и в

отсутствие ошибок демодуляции 1„ = 1„, где /„ означает продетектированное информационное значение одного символа /„ В этом случае sit;) в целом известна, за

исключением фазы несущей. Оценивание фазы, управляемое решениями (об информационных символах), было впервые описано Прокисом и др. (1964).

Для конкретности, рассмотрим оценивание фазы, управляемое решениями (ОУР, DDE), при линейной модуляции, когда принимаемый низкочастотный эквивалентный сигнал можно выразить так:

r{t) = -Z„git-nT) +zit) = 5,(/)e-* +z{t), (6.2.33)