s{t) = А coslnfj, 0<t<T,

где A-±\ с равными вероятностями. Ясно, что ФПВ для А равна

pU) = i5U-l)+i5U + l). Теперь функция правдоподобия Л(ф), определяемая (6.2.9), является условной при заданном значении А, к её следует усреднять по этим двум значениям. Таким образом,

л(ф) = £.л(ф)/7(Л) = ехр -\\{t)co4lTifjH)dt

ехр - -Jrit) софя/,/ + ф - ch -Jrii) co4lnfJ + ф/ а соответствующий логарифм функции правдоподобия

Л;(ф) - In ch -ЦгО) colnfJ + )dt

(6.2.44)

Если продифференцируем Л(ф) и приравняем производную нулю, получим МП

оценку для фазы, не управляемую решениями (оценивание, не управляемое решениями -ОНУР, NDDE). К сожалению, функциональное отношение в (6.2.44) существенно нелинейно, и, следовательно, точное решение трудно получить. С другой стороны, возможна аппроксимация. В частности,

.2/о

Inchx =

xii {]

(6.2.45)

[x«l

\\х\

С этой аппроксимацией решение для ф получается в трактуемом виде.

В этом примере мы усреднили по двум возможным значениям амплитуды информационных символов. Если информационные символы М-позиционные, а М велико, операция усреднения содержит нелинейные функции высокого порядка от параметра, который оценивается. В этом случае мы можем упростить проблему, предположив, что амплитуды информационных символов являются непрерывными случайными величинами. Например, мы можем предположить, что они подчиняются гауссовскому распределению с нулевым средним. Следующие примеры иллюстрируют эту аппроксимацию и результирующую форму для усредненной функции правдоподобия.

Пример 6.2.3. Рассмотрим тот же сигнал, что в примере 6.2.2, но теперь предположим, что амплитуда А является гауссовской, с нулевым средним и единичной дисперсией, т е.

р{А) =

Если мы усредним л(ф) по заданной ФПВ А, получим для усреднённой функции правдоподобия

Л(ф) = С ехр- r{i) colnfJ + ф) dt

и соответствующий логарифм усреднённой функции правдоподобия

- \-N~fo co4lnfJ + )dt]

(6.2.46)

(6.2.47)

Теперь мы можем получить МП оценку для ф путём дифференцирования Л(ф)и приравнивания результата нулю.

Интересно отметить, что логарифм усреднённой функции правдоподобия является квадратичным при гауссовском предположении, а также то, что он имеет квадратичную аппроксимацию, определённую (6.2.45), для.малых значений взаимной корреляции /(/) и

s{t; ф) . Другими словами, если взаимная корреляция на одном интервале мала, гауссовское предположение для распределения амплитуд информационных символов даёт хорошую аппроксимацию для логарифма усреднённой функции правдоподобия .

С точки зрения этих результатов мы можем использовать гауссовскую аппроксимацию на все символы на интервале КТ. Конкретнее, предположим, что К информационных символов статистически независимы и одинаково распределены. При усреднении функции правдоподобия л(ф) по гауссовской ФПВ на каждом из К символов на интервале 7 - КТ получаем результат

л(ф) = Сехр 2

n=OL

f(n+l)r пТ

(6.2.48)

Если мы возьмём логарифм от (6.2.48), продифференцируем его и приравняем результат нулю, получим условие для МП оценки в виде

Е£Гсоз(2л/,Г + ф)/£"(/)51п(2л/;/ + ф)/ = 0. (6.2.49)

Хотя это уравнение можно преобразовывать и дальше, уже его настоящая форма предполагает схему петлевого отслеживания, показанного на рис. 6.2.11. Эта петля похожа на петлю Костаса, которая будет описана ниже. Заметим, что произведение двух сигналов от интеграторов устраняет знак несущей, обусловленной информационными символами.

Входной сигнал

соз(2п +ф)

sin(2n +$)

Стробирующее

устройство t=nT

Стробирующее

устройство t=nT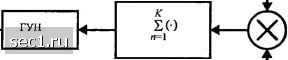

Рис. 6.2.11. ФАП, не использующая решения детектора для оценивания фазы AM сигналов

Сумматор играет роль петлевого фильтра. В петлевой схеме отслеживания сумматор можно реализовать или как цифровой фильтр со скользящим окном (сумматор), или как низкочастотный цифровой фильтр с экспоненциальным взвешиванием последних данных.

Подобным образом можно осуществить МП оценку фазы, не управляемую решениями, для КАМ и многопозиционной ФМ.

Исходная операция сводится к усреднению функции правдоподобия (6.2.91) по

статистике параметров данных. Здесь снова мы можем использовать гауссовскую аппроксимацию (двухмерное гауссовское распределение для комплексных информационных символов) или усреднение по информационной последовательности.

Квадратичная петля. Квадратичная петля - это петля, не управляемая решениями, которая широко используется на практике для установления фазы несущей в двухполосной системе с подавленной несущей, такой как AM. Чтобы описать её работу, рассмотрим проблему оценивания фазы несущей сигнала цифровой AM в виде

sit) = Ait) cos(27i/;/ + ф), (6.2.50)

где Ait) несёт цифровую информацию. Заметим, что = - О, когда

сигнальные уровни распределены симметрично относительно нуля. Следовательно, усреднённое значение sit) не может дать ни одной фазокогерентной частотной компоненты, исключая несущую. Один из методов восстановления несущей от принимаемого сигнала сводится к его квадратированию и, следовательно, к генерированию частотной компоненты 2/., которую можно использовать для образования

фазозамкнутой петли (ФЗП), настроенной на частоту 2/. Этот метод иллюстрируется блок-схемой, показанной на рис. 6.2.12.

Выход к когерентному демодулятору

sin(2)j4) <-

Делитель частоты ч-2

Петлевой фильтр

sin(4n/j+2$)

Рис. 6.2.12. Восстановление несущей с использованием квадратирующего устройства

Выход квадратичного устройства равен

s\t) - A\t)cos (iTtfJ + ф) = i At) +1 Ait) cos(4nfJ + 2ф). (6.2.51)

Поскольку модулированный сигнал является циклостационарным случайным процессом, математическое ожидание от sit) равно

И)] = ilW] +1£[ W] cos{4nfJ + 2ф). (6.2.52)

Следовательно, имеется мощность на частоте 2/..

Когда выход квадратирующего устройства проходит через полосовой фильтр, настроенный на удвоенную частоту в (6.2.51), среднее-значение на выходе фильтра - это

синусоида с частотой 2/, фазой 2ф и амплитудой 2Е Ait) н(2/, где я(2/ - усиление фильтра на частоте f -2f. Таким образом, квадратирующее устройство образует периодическую компоненту от входного сигнала t). По существу, квадратирование уничтожает знак информации, содержащейся в Ait) и таким образом приводит к фазо-