когерентной частотной компоненте на удвоенной частоте несущей. Фильтруемая компонента на частоте 2/, затем используется для управления ФЗП.

Операция квадратирования ведет к обогащению шума, что увеличивает уровень шумовой мощности на входе ФАП и ведёт к увеличению дисперсии фазовой ошибки.

Чтобы разобраться с этим вопросом, допустим, что на вход квадратирующего звена поступает сигнал s{t)+M,t), где s{t) определено (6.2.50), а nit) представляет полосовой аддитивный гауссовский шумовой процесс. При квадратировании sit)+n{i) получаем

y{t) = sit)+2sit)n{t) + n-{t) , (6.2.53)

где s-{t) - желательная сигнальная компонента, а две остальные компоненты - это слагаемые сигнал х шум и шум х шум. Вычислив автокорреляционную функцию и спектральную плотность мощности этих двух шумовых компонент, можно легко показать, что обе компоненты имеют спектральную плотность мощности в частотной полосе, сосредоточенной вблизи 2/,. Следовательно, полосовой фильтр с полосой В, центрированной на частоте 2/, который создает желательные синусоидальные компоненты сигнала, управляющие ФЗП, также пропускает шум, обусловленный двумя слагаемыми. Поскольку полоса петли рассчитывается так, чтобы быть существенно меньшей, чем полоса В полосового фильтра, суммарный спектр шума на входе ФЗП можно аппроксимировать константой на частотах внутри полосы петли. Такая аппроксимация позволяет нам получить простое выражение для дисперсии фазовой ошибки

a; = l/YA, (6-2.54)

где названа квадратичными потерями и определяется так:

S= \ + -- . (6.2.55)

Поскольку Si<\, Sj определяет увеличение дисперсии фазовой ошибки, вызванной дополнительным шумом (слагаемым шум х шум), обусловленным квадратированием. Заметим для примера, что, когда = пф/2экв потери составляют 3 дБ.

В заключение заметим, что выход ГУН в схеме с квадратированием необходимо делить по частоте на 2, чтобы генерировать синхронную несущую для демодуляции сигнала. Надо подчеркнуть, что выход делителя частоты характеризуется неоднозначностью фазы на 180° относительно фазы принимаемого сигнала. Из этих соображений двоичные данные следует дифференциально кодировать до модуляции и дифференциально декодировать в приёмнике.

Петля Костаса. Другой метод восстановления фазированной несущей для двухполосной системы с подавленной несущей иллюстрируется рис. 6.2.13. Эта схема была предложена Костасом (1956) и называется петлей Костаса

Принимаемый сигнал умножается на 003(271/"/ +ф) и im{lnfj + , которые являются

выходами ГУН. Получаем два произведения:

yXt) = W + rii)\coTifJ + ф) = i[(/) +иД?)]соз Аф +1«,(/) sin Аф +

+ слагаемое с двойной частотой, (6.2.56)

yi,t) = [At)+гЩ sin(27iX/ + ф) = \\a{i) + nJSi\ sin Лф + i ni,t) cos Аф + + слагаемое с двойной частотой,

где фазовая ошибка Аф = ф - ф. Слагаемое с удвоенной частотой устраняется фильтрами низких частот, расположенными после умножителей.

Фильтр НЧ

с08(2я/Г+ф)

Фазовращатель на 90°

Петлевой фильтр

Рис. 6.2.13. Блок-схема петли КЬстаса

Сигнал ошибки генерируется путем умножения двух выходов фильтров низких частот. Таким образом,

= i + nSt)f - nit)] 81п(2Аф) - UStpit) + иД/)]со5(2Аф). (6.2.57)

Этот сигнал ошибки фильтруется петлевым фильтром, выход которого управляет ГУН. Читатель может убедиться в похожести петли Костаса и петли ФЗП, показанной на рис. 6.2.11.

Заметим, что сигнал ошибки на входе петлевого фильтра состоит из желательного

слагаемого /4(/)51п2(ф-ф) и слагаемых, которые содержат сигнал х шум и шум х шум.

Эти слагаемые похожи на две шумовые слагаемые на входе ФЗП при использовании метода квадратирования. Действительно, если петлевой фильтр в петле Костаса идентичен тому, который используется в квадратичной петле, две эти петли эквивалентны. С учетом этого условия ФПВ ошибки фазы и качество этих двух схем ФАП идентичны.

Интересно заметить, что оптимальный ФНЧ для подавления слагаемых с двойной частотой в петле Костаса-это фильтр, согласованный с сигнальным импульсом информационной последовательности. Если согласованные фильтры используются как ФНЧ, их выходы можно стробировать с битовой скоростью в конце каждого сигнального интервала, а отсчёты в дискретных точках времени могут бьггь использованы для управления в петле. Использование согласованного фильтра ведет к меньшему шуму в петле.

В заключение заметим, что, как и в квадратичном ФЗП, выход ГУН в петле Костаса даёт неоднозначность фазы на 180°, что делает необходимым предварительное дифференциальное кодирование на передаче и дифференциальное декодирование после детектора.

Оценка несущей в системах с многопозиционными сигналами. Когда цифровая информация передается посредством М-позиционной модуляции фазы несущей, методы, описанные выше, можно обобщить, чтобы получить хорошую сфазированную несущую в

демодуляторе. Принимаемый М-фазный сигнал, исключая аддитивный шум, можно выразить так:

, /«=1,2,М,

(6.2.58)

At) = А cos[27i/;/ + ф +-{т -1)

где 2к(т -1) / Л/ представляет информационную компоненту фазы сигнала. Проблема восстановления несущей сводится к устранению информационной компоненты фазы и, как следствие, получению немодулированной несущей софтс/"/+ ф). Один из методов, при

помощи которого это можно сделать, иллюстрируется на рис. 6.2.14, который представляет обобщение петли с квадратированием. Сигнал проходит через устройство возведения в М-ю степень, которое генерирует определённое число гармоник

Полосовой фильтр выбирает гармонику conM/j + Мф) для управления ФЗП. Слагаемое информационной компоненты фазы сигнала

(m-l)M = 2Tiim-l)0 (mod2л), /и = 1,2,М

Принимаемый сигнал

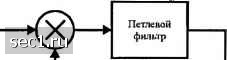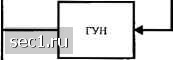Делитель частоты ш

викоя.

Рис. 6.2.14. Восстановление несущей с использованием

устройства возведения в М-ю степень для Мпозищюнной ФМ

Таким образом, информация устранена. Выход ГУН-это sin этот

выход делится по частоте на М дпя получения sin(27t/"/+ф) и сдвигается на 90° для

получения cos(27t/"/+ф). Эта компонента затем подаётся на демодулятор. Нетрудно показать, что имеется неоднозначность в этих упомянутых синусоидах на 260°/М, которую можно преодолеть дифференциальным кодированием данных на передаче и дифференциальным декодированием после демодуляции на приёме.

Как в случае квадратичной ФЗП, полиномиальная ФЗП работает в присутствии шума, возрастающего после прохождения через устройство возведения в М-ю степень, которое

даёт на выходе сигнал y{t) - s{t)-i-n{t)

ш