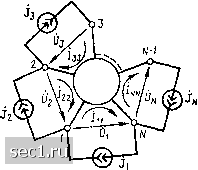Рис. 8.6. К выводу основных уравнений многополюсника в форме Z

подключенных между выводами многополюсника (рис. 8.6, а). В соответствии с принципом наложения, напряжения между внешними выводами линейного неавтономного многополюсника (У,- \foryT быть представлены в виде суммы частичных напряжений Щ1\ вызванных

действием каждого из независимых источников тока Jj в отдельности:

(8.11)

(In = + ... + f/ =Zs, h +N2 + +Znn h.

Коэффициенты системы уравнений (8.11) на.чываются параметрами холостого хода, или Z-n араметрами, многополюсника и имеют физический смысл входных

z,juriJi

(8.12)

или передаточных

Zi} = U\lJj (8.13)

комплексных сопротивлений, определенных в режиме, когда все источники тока, кроме Jj, выключены (рис. 8.6, б). Заменяя в уравнениях (8.11) источники тока контурными токами соответствующих контуров и используя матричную форму записи, получаем основные уравнения многополюсника в форме Z:

Zji Z22 ... Z2N

Zni Zn2--- Znn

12 Зак. 565

(8.14)

Квадратная матрица

Zji ••. ZlN

Z21 Z22 ... Z2Ar

Zwi Zw2-.- Zww

стоящая в правой части уравнений (8.14), называется неопределенной матрицей сопротивлений, или неопределенной матрицей Z-параметров, многополюсника*.

Неопределенную матрицу сопротивлений можно рассматривать как обобщенный параметр многополюсника,устанавливающий связь напряжений между выводами многополюсника с контурными токами внешних по отношению к не.му контуров. Элементы неопределенной матрицы сопротивлений определяются в соответствии с их физическим смыслом по результатам опытов холостого хода, причем сумма элементов каждого столбца и сумма элементов каждой строки матрицы 2г равны нулю.

• ••••

Пример 8.2. Найдем неопределенную матрицу сопротивлений биполярного транзистора, низкочастотная схема замещения которого по переменному току в режиме малого сигнала приведена на рис. 1.19, а.

Присвоим выводам эмиттера, коллектора и базы соответственно номера 1, 2, 3 и построим комплексную схему замещения транзистора, на которой укажем положительные направления напряжений между выводами и положительные направления контурных токов внешних по отношению к транзистору контуров (рис. 8.7, а). Основная cucme.ua уравнений рассматриваемого многополюсника в форме Z

содержит девять неизвестных коэффициентов-Z-параметров транзистора, для определения которых необходимо произвести три опыта холостого хода. Схемы опытов холостого хода, позволяющих найти частичные напряжения между выводами транзистора, вызванные действием каждого из источников тока - ~ Ai> -2 ~ 22 и J3 = /33 в отдельности, приведены на рис. 8.7, б, в, г соответственно. Отношения чатичных напряжений к токам вызвавших их источников тока согласно (8.12), (8.13) представляют собой искомые параметры:

= OS"/Л=/?э+/?б; = tyV/Л=Rm-Rb,

£з2 =Ui4Ji=Rra-RH. Zss=Ui4JzR6+R.

*) Неопределенные матрицы сопротивлений и проводимостей многополюсника Zij и Yг не следует путать с матрицами контурных сопротивлений Z(i) и узловых проводимостей Y(j.

\1 Т "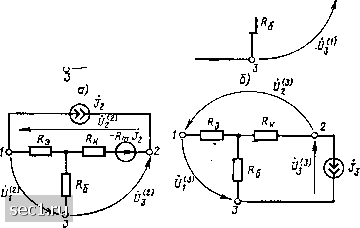

Рис. 8.7. К примеру 8.2

Можно убедиться, что сумма элементов любой строки, как и сумма элементов любого столбца неопределенной матрицы сопротивлений биполярного транзистора ,

Zij = 2

/?э + /?б

-Ro Ru-i- Rs-Rn

Rm-RK

-Re R6+R« J

равна нулю.

При построении основных уравнений многополюсника в формах Y или Z в качестве независимых переменных выбирались либо только напряжения, либо только токи, связанные с внешними выводами. В каждом из этих случаев коэффициенты основной системы уравнений имели одинаковую размерность и определялись в одном и том Же режиме (короткого замыкания или холостого хода). Системы первичных параметров многополюсника, в которых все параметры имеют одинаковую размерность и определяются в одинаковом режиме, называются однородными.

Если в качестве независимых переменных выбрать токи одних, а напряжения других сторон многополюсника, то коэффициенты полученной системы уравнений будут иметь различную размерность и определяться в различных режимах, причем часть недиагональных элементов соответствующей матрицы параметров может оказать-